6.4 Verschiebung in x-Richtung

Unsere Basisfunktionen zur Herleitung von Eigenschaften beliebiger quadratischer Funktionen ist bekanntlich  \(f:x \mapsto y =x^2\) mit ihrem Graphen, der Normalparabel.

Die Analyse geeigneter Funktionen zeigt dabei sehr schnell

• wie wir die Verschiebung in x-Richtung am Funktionsterm zielsicher erkennen
• und den Graphen der verschobenen Funktion sicher zeichnen können.

 

Aufgabe

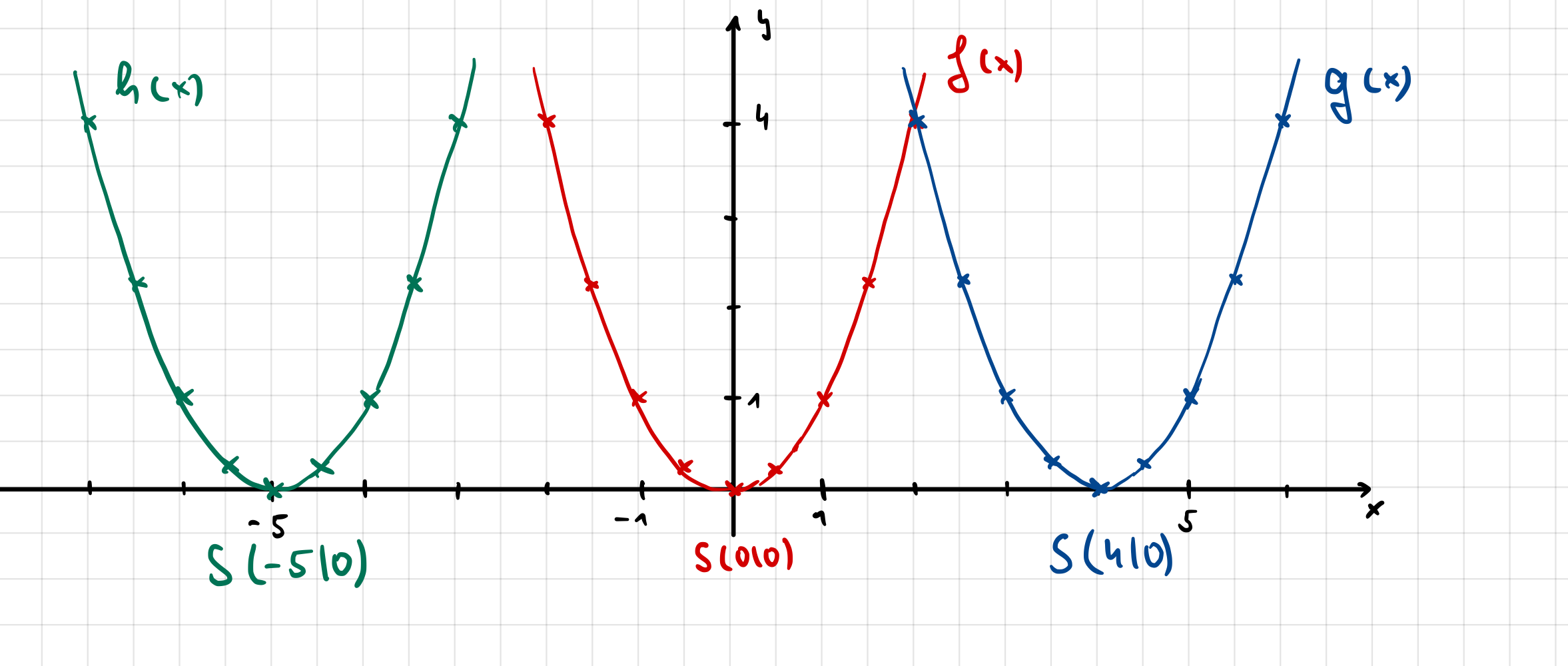
Gegeben sind die Funktionsterme \(f(x)=x^2\),  \(g(x)=(x-4)^2\) und \(h(x)=(x+5)^2\).

1. Für welche x-Werte liefern die Funktionsterme jeweils das Ergebnis null?
2. Welchen speziellen Punkt des jeweiligen Graphen verbindest du mit diesem Ergebnis?
   Gib für alle Terme jeweils die Koordinaten dieses Punktes an!
3. Erstelle mit diesen Erkenntnissen jeweils eine Wertetabelle für die Funktionsterme \(g\) und \(h\), mit der du die zugehörigen Graphen sehr genau zeichnen kannst.
4. Zeichne alle drei Graphen in ein gemeinsames Koordinatensystem.
   Platzbedarf in x-Richtung: -8 < x < +7
    
5. Beschreibe mit Hilfe zweier neuer Beispielterme, woran du erkennst, in welche Richtung ein Funktionsgraph gegenüber der Normalparabel verschoben ist und wie du den Graphen dann in ein Koordinatensystem zeichnest.

 

Ergebnis und Hefteintrag

 

6.4 Verschiebung in x-Richtung

Gegeben sind die Funktionsterme \(f(x)=x^2\), \(g(x)=(x-4)^2\) und \(h(x)=(x+5)^2\).

Die vorgegebenen Funktionen liefern jeweils für einen speziellen Wert \(x_0\) den Funktionswert \( 0 \) . Es handelt sich dabei um die Nullstelle der Funktion. Der zugehörige Punkt ist der Scheitel \(S\) der Parabel.

Funktion	Nullstelle	Scheitel
\(f(x)=x^2\)	\(x_0=0\)	\(S(0|0)\)
\(g(x)=(x-4)^2\)	\(x_0=4\)	\(S(4|0)\)
\(h(x)=(x+5)^2\)	\(x_0=-5\)	\(S(-5|0)\)

Sinnvoll ist es, wenn wir die Wertetabellen für x-Werte aufbauen, die symmetrisch links und rechts des Scheitels liegen.

\(f(x)=x^2\)

x	-3	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2	3
y=f(x)	9	4	2,25	1	0,25	0	0,25	1	2,25	4	9

 

\(g(x)=(x-4)^2\)

x	1	2	2,5	3	3,5	4	4,5	5	5,5	6	7
y=f(x)	9	4	2,25	1	0,25	0	0,25	1	2,25	4	9

 

\(h(x)=(x+5)^2\)

x	-8	-7	-6,5	-6	-5,5	-5	-4,5	-4	-3,5	-3	-2
y=f(x)	9	4	2,25	1	0,25	0	0,25	1	2,25	4	9

 

Wir erkennen:
Symmetrisch um den x-Wert des Scheitels erhalten wir bei allen Funktionen die selben Funktionswerte. Zum Zeichnen der jeweiligen Funktion müssen wir uns daher lediglich den Scheitel überlegen und die Funktionswerte der Normalparabel \(f(x)=x^2\) kennen und ausgehend vom Scheitel in das Koordinatensystem eintragen.

 

Entwicklung der Graphen

 

Regel:

Auf Grundlage der Wertetabelle mit den Funktionswerten für die Funktion \(f:x \mapsto f(x)=x^2\) der Normalparabel erkennen wir folgenden Zusammenhang:

Der Graph \(G_f\) der Funktion \(f:x \mapsto y=(x-d)^2\) mit \(d \in R\) entsteht aus der Normalparabel durch Verschiebung in x- Richtung. Verschiebung um \( d \)  nach rechts, falls  \(d>0\) Verschiebung um \( |d| \) nach links, falls  \(d<0\) Der Graph \(G_f\) hat also die Form der Normalparabel mit dem Scheitel \(S (-d | 0) \).

Aufgaben:

Bestimme von folgenden Funktionen jeweils den Scheitel und zeichne die Graphen in ein Koordinatensystem ein:

• \(f(x)=(x-3)^2\)
• \(g(x)=(x+4)^2\)
• \(h(x)=x^2-5\)
• \(k(x)=x^2+1\)