1.4 Die Menge der reellen Zahlen IR

 

Im letzten Kapitel haben wir festgestellt, dass beispielsweise \(\sqrt{2} \) keine rationale Zahl ist und daher nicht als Bruch darstellbar ist. Das Gleiche gilt für \( \sqrt{3}, \sqrt{5},\sqrt{11}\)  usw.

 

Lücken auf der Zahlengeraden

Unsere bisher bekannte Zahlenmenge, die Menge der rationalen Zahlen \(Q\), kann also unsere Zahlengerade nicht vollständig auffüllen.

Würden wir unsere Zahlengerade unter einem starken Mikroskop betrachten, so kämen Lücken an den Orten der irrationalen Zahlen ans Licht, die wir natürlich füllen müssen.

Mit der Menge der irrationalen Zahlen  können diese Lücken nun geschlossen werden!

  

Beispiele für bestehende Lücken auf unserer Zahlengeraden:

 

Erweiterung unseres Zahlenbereichs \(Q\)

 

 

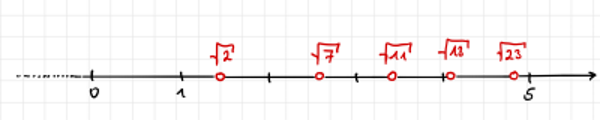
Die reellen Zahlen Die Menge IR der reellen Zahlen besteht aus den rationalen Zahlen und der Menge der irrationalen Zahlen. Die Menge der rationalen Zahlen \(Q\) besteht aus allen Zahlen, die durch einen Bruch \( \large \frac{z}{n}\)  mit  \(z \in Z\)  und  \(n in N\) darstellbar sind. Es gibt aber auch Zahlen, die sich nicht als Bruch darstellen lassen, die also nicht rational sind. Diese Zahlen nennt man irrationale Zahlen.   Übersicht der bekannten Zahlenmengen:

 

 

---

Übung zu Quadratwurzeln:		Link zu Serlo
Zusammenfassung