1.5 Ereignisalgebra

Bereits im Kapitel 1.4 Ereignisse haben wir bereits angesprochen, dass unterschiedliche Ereignisse gleichzeitig eintreten können, wenn ein Ergebnis eines Zufallsexperiments ein Element verschiedener Ereignisse ist.

Diese Verknüpfung von Ereignissen wird mit Hilfe von VENN-Diagrammen und der Ereignisalgebra beschrieben.

Beschreibung	Schreibweise	Darstellung
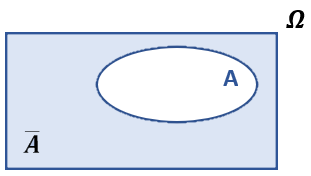
Gegenereignis zu A nicht A \(\small \overline{A}\) tritt ein wenn \( \small A\) nicht eintritt	\( \small \overline{A} \)
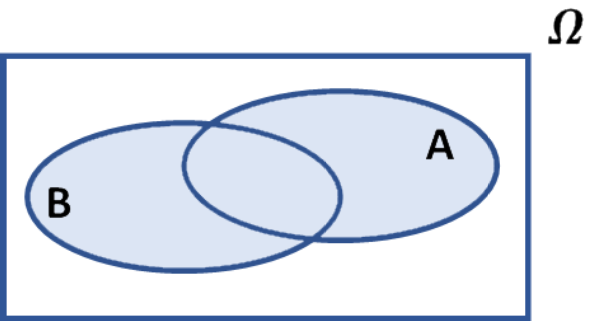
Vereinigungsmenge A oder B tritt ein \( \small A \cup B\) tritt ein, wenn A oder auch B eintritt	\( \small A \cup B\)
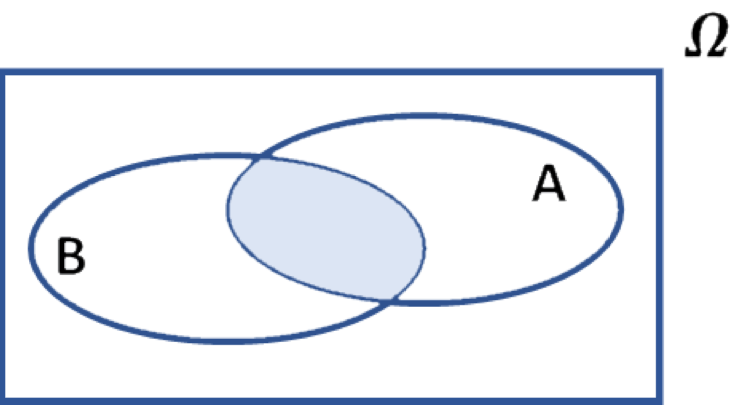
Schnittmenge A und gleichzeitig B treten ein A und B \(\small A \cap B\) tritt ein, wenn A und zugleich B eintritt	\(\small A \cap B\)
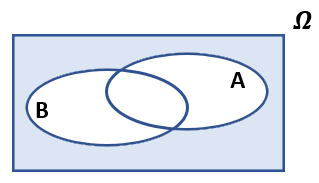
nicht A und nicht B \(\small  \overline {A} \cap \overline {B} \) tritt ein, wenn keines der beiden Ereignisse A und B eintritt	\(\small \overline{A} \cap \overline{B} = \overline{A \cup B} \)
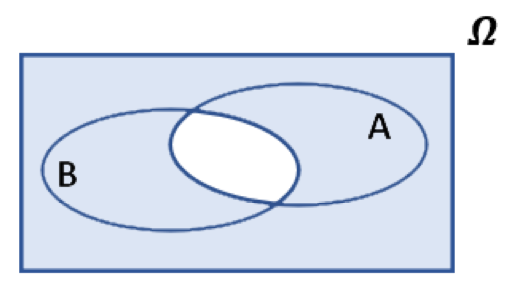
nicht A oder nicht B \(\small \overline{A} \cup \overline{B} \) tritt ein, wenn höchstens eines der beiden Ereignisse A und B eintritt.	\(\small \overline{A} \cup \overline{B} = \overline{A \cap B} \)

 

 

Ein Beispiel zur Erklärung

Beim einfachen Würfelwurf erhalten wir den Ergebnisraum \( \small \Omega = \{1; \space 2; \space 3; \space 4; \space 5; \space 6 \}\).

Uns interessieren die geworfenen Augenzahlen hinsichtlich der folgenden Ereignisse

\(\small A=\{2; \space 4 \} \);  \(\small B=\{2; \space 6 \} \)  und  \(\small C=\{2; \space 4;  \space 6\} \)

und bilden nachfolgende kombinierte Ereignisse nach den Gesetzen der Mengenalgebra:

\( \small \overline{A}= \{1; \space 3; \space 5; \space 6 \}\) \( \small \overline{B}= \{1; \space 3; \space 4; \space 5 \}\) \( \small \overline{C}= \{1; \space 3; \space 5\}\) \( \small A \cup B = \{2; \space 4; \space 6\}\) \( \small A \cap B = \{2\}\) \( \small \overline{A} \cup B = \{1; \space 2; \space 3;\space 5; \space 6\}\)

\( \small \overline{A} \cap B = \{ 6\}\) \( \small A \cup \overline{B} = \{1; \space 2; \space 3; \space 4; \space 5 \} \) \( \small A \cap \overline{B} = \{4\} \) \( \small \overline{A} \cup \overline{B}=\{1; \space 3; \space 4; \space 5; \space 6 \} \) \( \small \overline{A} \cap \overline{B}=\{1; \space 3; \space 5\} \) \(\small A \cap B \cap C = \{2\} \)

 

 

---