2. Der Begriff der Wahrscheinlichkeit

Im 1. Kapitel beschäftigten wir uns mit der Definition und den Grundlagen sogenannter Zufallsexperimente. Für jegliche Art solcher Experimente muss uns in einem nächsten Schritt die Wahrscheinlichkeit interessieren, mit der ein bestimmtes Ergebnnis eintreten wird.

Dabei kann aufgrund logischer Zusammenhänge ein mathematisches Modell für ein vorliegendes Zufallsexperiment entwickelt werden. Falls dies nicht möglich ist, wird mit einer ausreichend langen Versuchsreihe mit Hilfe der relativen Häufigkeit eine empirische Wahrscheinlichkeit für ein Ergebnis bestimmt.

Die Zusammenhänge zwischen Realität und mathematischen Gesetzmäßigkeiten lassen sich anhand der Grafik veranschaulichen:

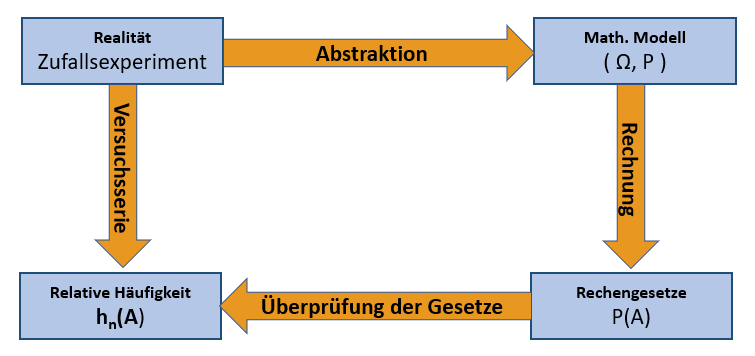
• In der Realität wird ein Zufallsexperiment aufgrund von Erfahrungen abstrahiert in ein mathematisches Modell und den Ergebnissen werden dabei entsprechende Wahrscheinlichkeiten zugeordnet.
   
  \( \hspace{10mm}\) Bsp.: Münzwurf:  \(\small  \Omega = \{K; \space Z\}\)  mit  \(\small P('K')=P('Z')=\frac{1}{2} \)
   
• Auf dieses Modell können Rechengesetze entwickelt oder angewandt werden.
• Das mathematische Modell und die Rechengesetzen eignet sich jedoch nur, wenn die Überprüfung mit Hilfe der relativen Häufigkeit  diese betätigt.
• Andererseits kann die Wahrscheinlichkeitsverteilung der Ergebnisse eines Zufallsexperiments mit Hilfe einer ausreichend langen Versuchsreihe über die relative Häufigkeit plausibel gemacht werden.

 

---