7.9 Monotonie von Funktionen (Wiederholung)

Grundsätzlich muss die Untersuchung der Monotonie beliebiger Funktionen fester Bestandteil der Kurvendiskussion sein. Mit den Ergebnissen dieser Analyse ist man in der Lage schnell Rückschlüsse auf den Verlauf eines Funktionsgraphen zu ziehen und diesen mit den weiteren Ergebnissen der Kurvendiskussion wie Definitionslücken, Achsenschnittpunkte, Verhalten an den Grenzen des Definitionsbereiches usw., schnell zu skizzieren.

Bestimmung des Monotonieverhaltens:
Man bestimmt das Monotonieverhalten einer differenzierbaren (ableitbaren) Funktion \(f\) in der Regel über deren erste Ableitung \(f'\).

Mit Hilfe der Ableitung kann man herausfinden in welchen Bereichen der Graph \(G_f\) einer Funktion \(f\)
(streng) monoton steigend oder (streng) monoton fallend ist.

• Falls \(f'(x) \geq 0 \hspace{1em} \Longleftrightarrow \hspace{1em} \) Funktion \(f\) ist monoton steigend
• Falls \(f'(x) \leq 0 \hspace{1em} \Longleftrightarrow \hspace{1em} \) Funktion \(f\) ist monoton fallend

 

Die Monotonieintervalle lassen sich mit zwei Methoden festlegen:

• Monotonietabelle:
  - Das Vorzeichen der Ableitung wird im Definitionsbereich bestimmt.
  - Vorsicht: Nullstellen der Ableitung und Definitionslücken müssen beachtet werden.
  
  
•  Analyse der 2. Ableitung \(f''\) einer Funktion
  - Über das Vorzeichen der 2. Ableitung schießt man auf die Art der Extremstellen
  - und schließt dann auf das Monotonieverhalten (Vorzeichen von \(f'\).
  - Nachteil: Sehr abstrakt und die 2. Ableitung ist mitunter kompliziert.

 

Unterschiedliche Typen der Monotonie von Funktionen

Grundsätzlich unterscheidet man vier Typen der Monotonie, die durch folgende Beispiele veranschaulicht werden. Die strenge Monotonie schließt waagerechte Bereiche einer Funktion aus. Sie verlang, dass eine Funktion stets steigt oder fällt und ist damit eine stärkere Eigenschaft als die Monotonie.

Für jede differenzierbare (ableitbare) Funktion \(f\)  kann die Art der Monotinie mit dem Vorzeichen der ersten Ableitung \(f'\) charakterisiert werden.

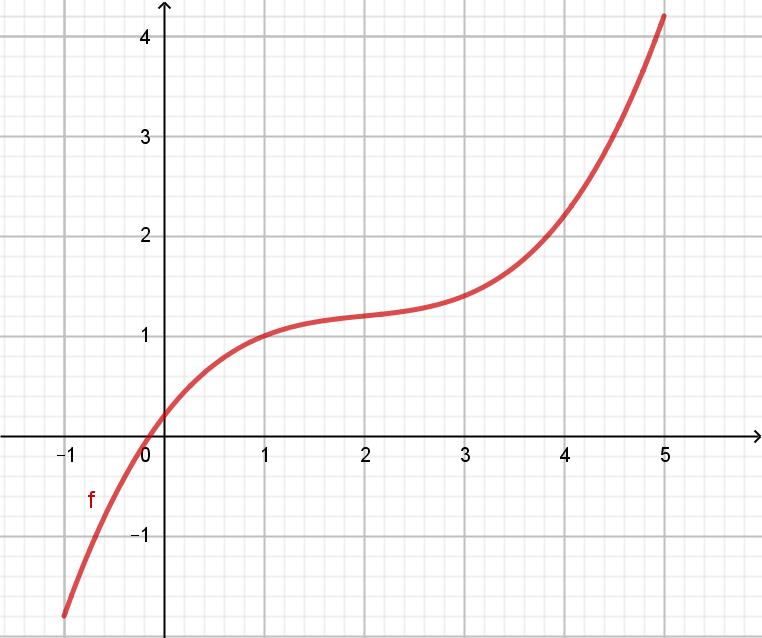
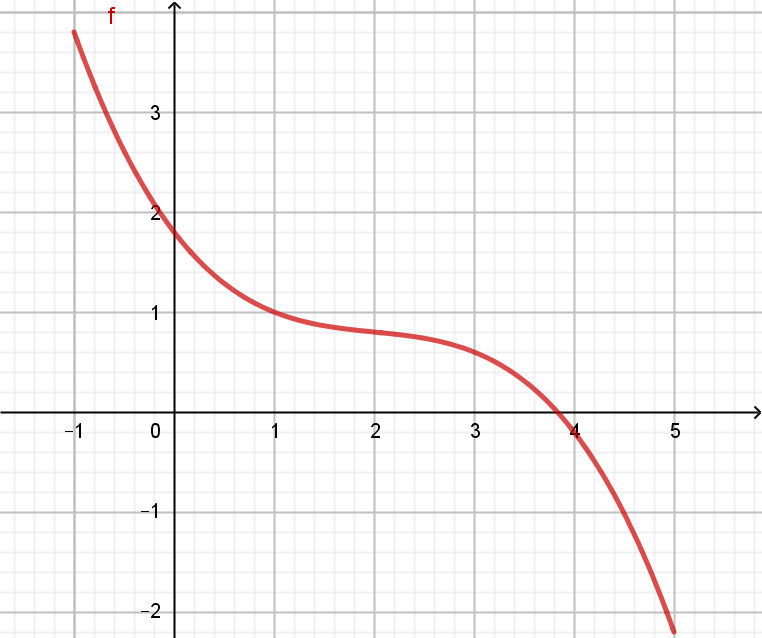
streng monoton steigende Funktion \(f'(x)>0 \Leftrightarrow f \) ist streng monoton steigend	streng monoton fallende Funktion \(f'(x)<0 \Leftrightarrow f \) ist streng monoton fallend
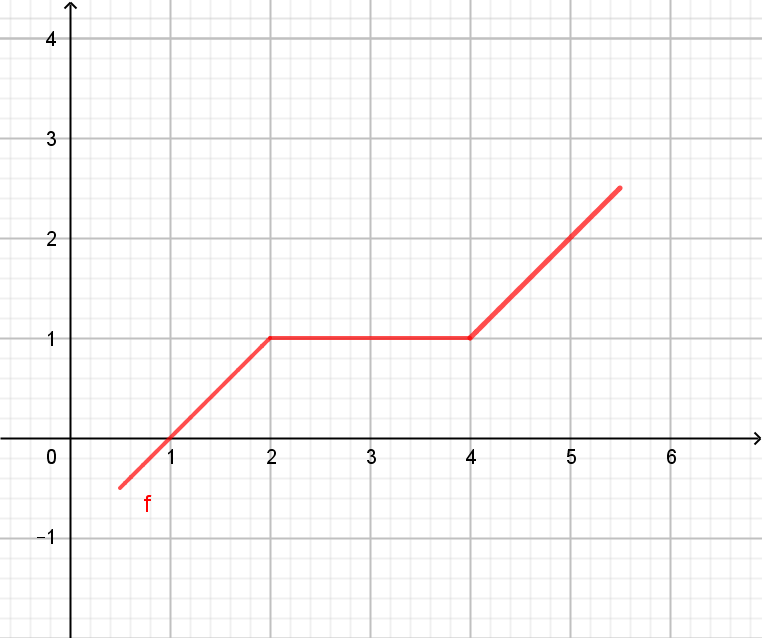
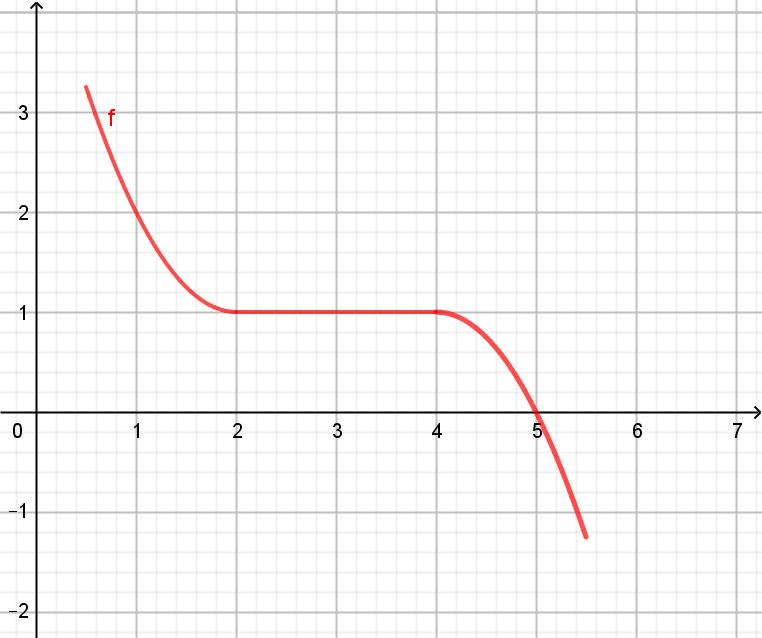
monoton steigende Funktion \(f'(x) \geq 0 \Leftrightarrow f \) ist monoton steigend	monoton fallende Funktion \(f'(x) \leq 0 \Leftrightarrow f \) ist monoton fallend

Monotonieintervalle

In der Regel wechseln Funktionen auf ihrem Definitionsbereich ihr Monotonieverhalten. Es gibt also unterschiedliche Bereiche, in denen eine Funktion (streng) monoton fällt oder (streng) monoton steigt.

Für die nachfolgende Funktion \(f\) lassen sich beispielsweise drei Monotoniebereiche festlegen. 

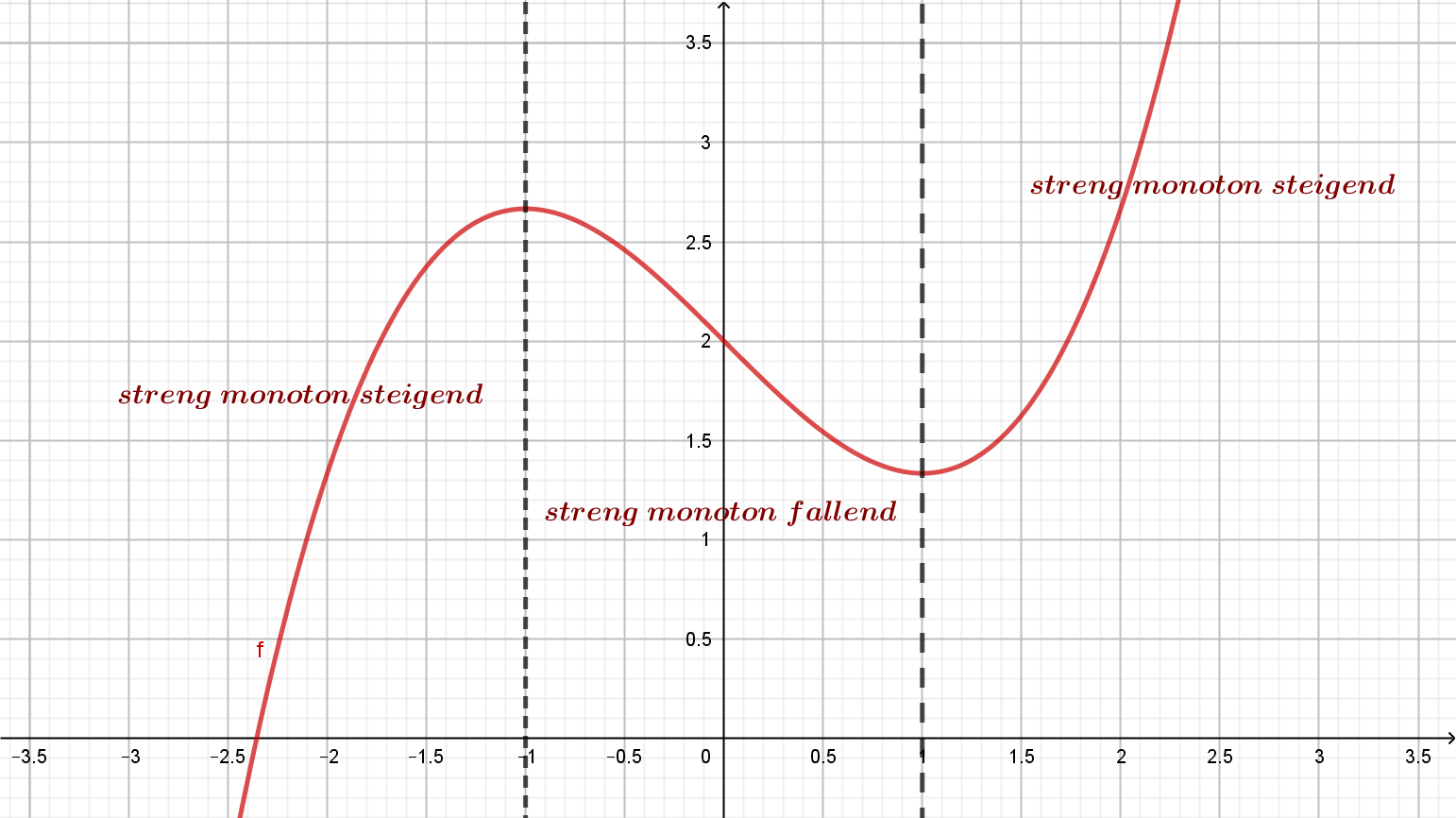
Auf Basis der Festlegung der Monotoniebereiche, die sich durch die systematische Monotoniebetrachtung ergeben, lassen sich Lage und Art der Extremstellen von Funktionsgraphen bestimmen.

 

---

Arbeitsblätter, Übungen und Lösungen zu den Stoffgebieten

---

Bezeichnung