9.1 Bedeutung der ersten und zweiten Ableitung
Die erste Ableitung
Die erste Ableitung \(f'\) einer Funktion \(f\) liefert uns stets die Steigung einer Tangente t in einem beliebigen Punkt \(x_0\) auf dem Graphen \(G_f\).
 |
Die Abbildung verdeutlicht die Bedeutung der ersten
Ableitung. Die rote Strecke zeigt einen Ausschnitt der Tangente im
Punkt P an den Graphen \(G_f\). Für die Steigung er Tangeten gilt: \(m_t=f'(x_0)\) |
Mit der ersten Ableitung können wir eine Funktion \(f\) auf ihr Monotonie-Verhalten untersuchen:
Definition des Monotonieverhaltens:
Gegeben ist eine
Funktion \(f\) mit ihrem Definitionsbereich \(D_f\). Für die Monotonie der
Funktion \(f\) in einem Teilintervall \(I\) des Definitionsbereiches gilt
dann:
- Ist \(f'(x) > 0\) für alle \(x \in I \hspace{1em} \Leftrightarrow\ \hspace{1em}\) f ist streng monoton steigend
- Ist \(f'(x) < 0\) für alle \(x \in I \hspace{1em} \Leftrightarrow\ \hspace{1em}\) f ist streng monoton fallend
Zusätzlich können wir die Funktion auf lokale Extremstellen bzw. Wendepunkte untersuchen:
- Falls \(f'(x_0) = 0 \hspace{0.5em} \Leftrightarrow\
\hspace{0.5em}f(x_0)\) hat an \(x_0\) eine lokale Extremstelle
oder einen Wendepunkt
- Ändert sich an \(x_0\) das Monotonieverhalten (von steigend auf fallend oder von fallend auf steigend) dann liegt eine lokale Extremstelle vor. Die erste Ableitung ändert also an \(x_0\) das Vorzeichen.
Die zweite Ableitung
Mit der zweiten Ableitung \(f''\) einer Funktion \(f\) können wir das Krümmungsverhalten einer Funktion untersuchen.
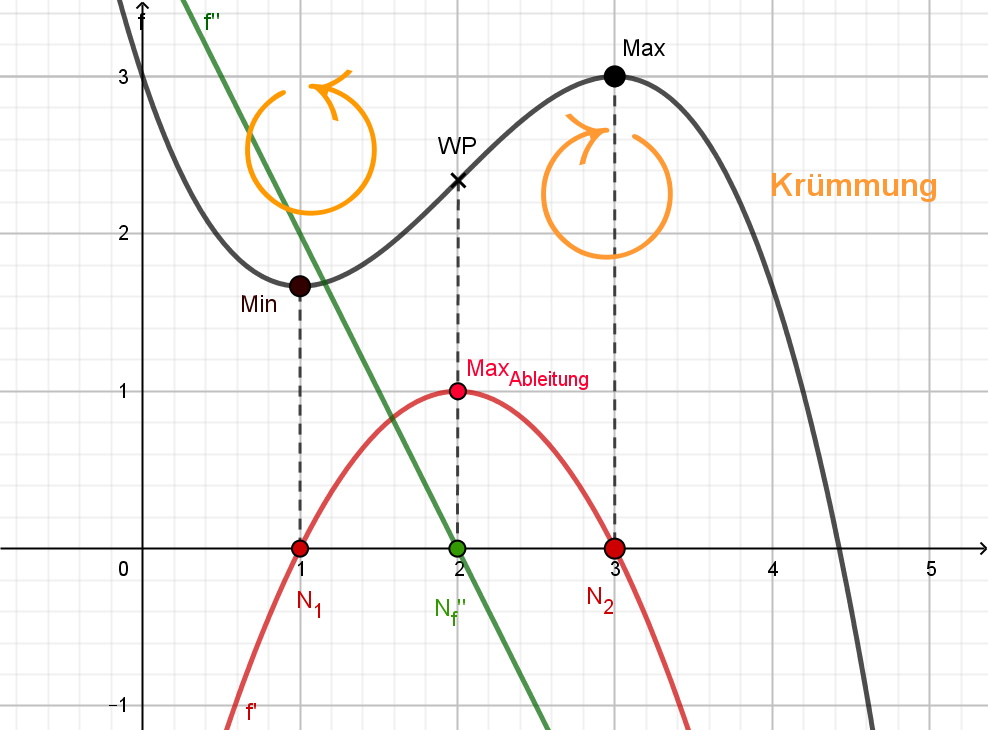 |
Die Abbildung stellt die Zusammenhänge zw.
Funktion, erster Ableitung und zweiter Ableitung dar. Die erste Ableitung liefert die jeweilige Steigung des Graphen der Funktion. An den Nullstellen \(N_1\) und \(N_2\) der ersten Ableitung hat der Graph seine Extremstellen \(Min\) und \(Max\) und am Maximum der Ableitung \(Max_{Abl.}\) hat die Funktion ihre steilste Stelle \(\small WP\). |
Die zweite Ableitung anlysiert einerseits die erste Ableitung und liefert deren Steigung und andererseits können wir dadurch Rückschlüsse auf den Verlauf des Graphen der Funktion \(f\) ziehen.
- Der Graph der zweiten Ableitung fällt streng monoton bis \(N_{f''}\) . Seine y-Werte sind positiv, werden jedoch stets geringer!
- D.h. der Graph der ersten
Ableitung steigt bis zu dieser Stelle, die Steigung
nimmt aber stetig ab.
- Für den Graphen der Funktion bedeuted dieses Verhalten der Ableitung, dass seine Steigung immer größer wird, bis zu einem maximalen Wert am Punkt \(WP\).
- Dies äußert sich in seiner Linkskrümmung!
- Nach der Nullstelle \(N_{f''}\)
der zweiten Ableitung drehen sich diese Überlegungen um
und der Graph der Funktion \(f\) bekommt eine
Rechtskrümmung.
- Die Nullstelle der zweiten Ableitung \(N_{f''}\) liefert uns den x-Wert des Wendepunktes der Funktion.
Definition des Krümmungsverhaltens:
Gegeben ist eine
Funktion \(f\) mit ihrem Definitionsbereich \(D_f\). Für die Krümmung der
Funktion \(f\) in einem Teilintervall \(I\) des Definitionsbereiches gilt
dann:
- Ist \(f''(x) > 0\) für alle \(x \in I \hspace{1em} \Leftrightarrow\
\hspace{1em}\) f ist linksgekrümmt
\( \huge \curvearrowleft \)
- Ist \(f''(x) < 0\) für alle \(x \in I \hspace{1em} \Leftrightarrow\ \hspace{1em}\) f ist rechtsgekrümmt \( \huge \curvearrowright \)
Ergebnis:
Hat die
zweite Ableitung \(f''(x)\) einer Funktion \(f(x)\) eine Nullstelle \(x_0\)
mit Vorzeichenwechsel, dann ändert der Graph \(G_f\) der Funktion an dieser
Stelle \(x_0\) sein Krümmungsverhalten. Es existiert somit der Wendepunkt
\[WP(x_0 | f(x_0))\].
Video: Zusammenhang der Ableitungen
Arbeitsblätter, Übungen und Lösungen zu den Stoffgebietentrong>
| Bezeichnung | ||