

Grundsätzlich sind Nullstellen diejenigen x-Werte, für die ein Funktionsterm \(f(x)=0\) wird. Wir erhalten also stets die x-Stellen, an denen der Graph der Funktion \(f(x)\) die x-Achse "schneidet".
Eine quadratischen Funktion kann maximal zwei Nullstellen aufweisen!
Je nach Lage des Graphen im Koordinatensystem kennen wir drei Fälle:
|
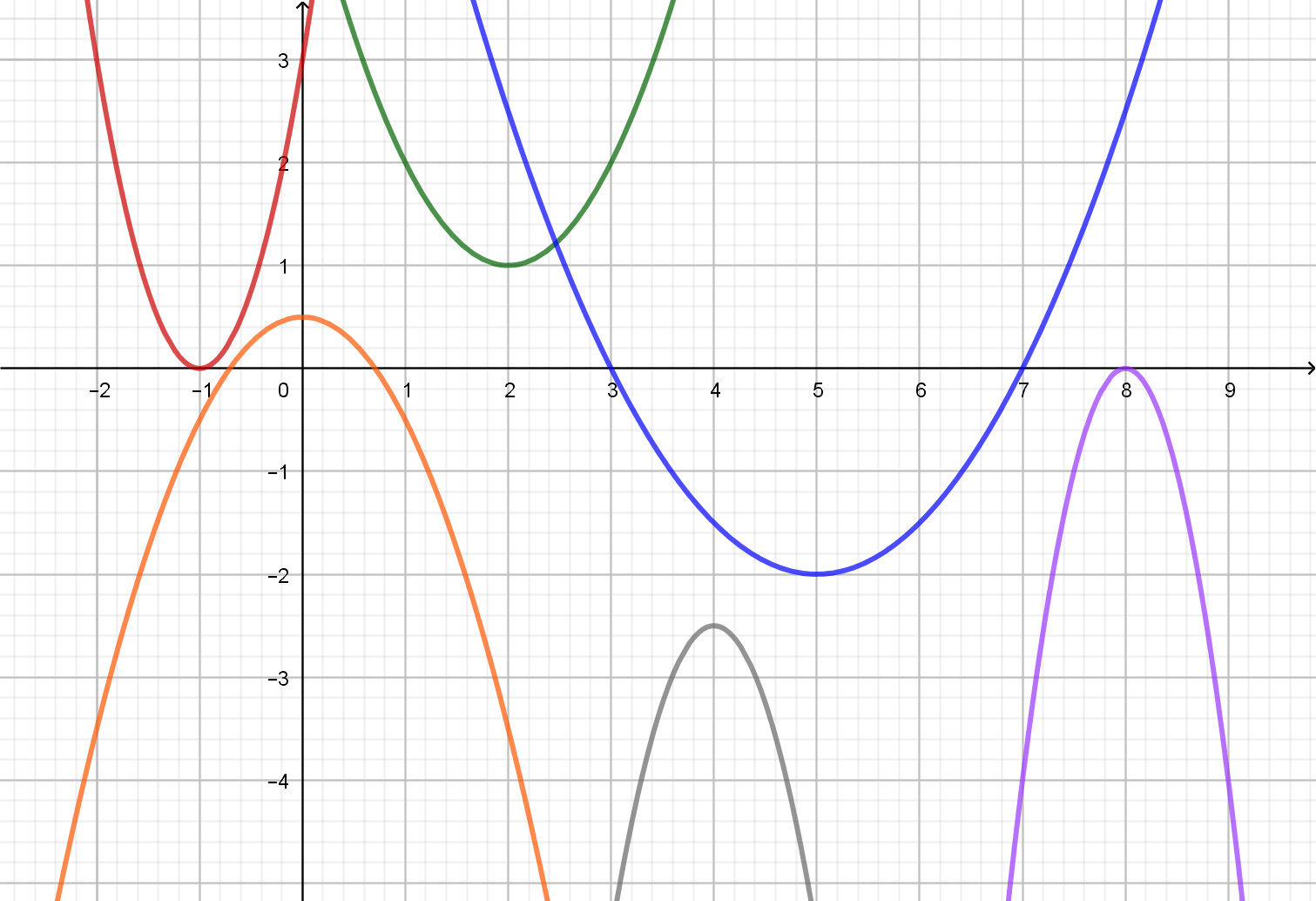 |
Video: Nullstellen quadratischer Funktionen
Anmerkung zum Video:
Das Video gibt einen guten
Überblick über die Lage des Funktionsgraphen im Koordinatensystem und der
Anzahl der vorhandenen Nullstellen. Ab der Berechnung der Nullstellen
unterscheidet sich der beschriebene Weg von unsere Vorgehensweise.
| Beispiel: | \(f(x)=2x^2-2x-4 \) |
| Ansatz: | \(f(x)=0 \hspace{1cm} \Leftrightarrow \hspace{1cm} 2x^2-2x-4=0\) |
| Mitternachtsformel: | \(x_{1/2}= \frac{-b
\pm \sqrt{b^2-4ac}}{2a}= \frac{2 \pm \sqrt{4-4 \cdot 2 \cdot (-4)}}{4}= \frac{2 \pm \sqrt{36}}{4}\) |
| Nullstellen: | Die
Diskriminante \(D=b^2-4ac\) der Lösungsformel ist positiv.
Die Gleichung hat daher zwei Lösungen und die vorliegende Funktion somit zwei Nullstellen! \(x_1=-1\) und \(x_2=2\) |
| Funktionsgraph: |
|
| Beispiel: | \(f(x)=-2x^2+8x-8 \) |
| Ansatz: | \(f(x)=0 \hspace{1cm} \Leftrightarrow \hspace{1cm} -2x^2+8x-8=0\) |
| Mitternachtsformel: | \(x_{1/2}= \frac{-b
\pm \sqrt{b^2-4ac}}{2a}= \frac{-8 \pm \sqrt{64-4 \cdot (-2) \cdot (-8)}}{-4}= \frac{-8 \pm 0}{-4}\) |
| Nullstelle: | Die
Diskriminante \(D=b^2-4ac\) der Lösungsformel ist null.
Die Gleichung hat daher genau Lösung und die vorliegende Funktion hat nur eine Nullstelle! \(x_{1/2}=2\) |
| Funktionsgraph: |
|
| Beispiel: | \(f(x)=-0.5x^2+2x-3 \) |
| Ansatz: | \(f(x)=0 \hspace{1cm} \Leftrightarrow \hspace{1cm} -0.5x^2+2x-3=0\) |
| Mitternachtsformel: | \(x_{1/2}= \frac{-2
\pm \sqrt{b^2-4ac}}{2a}= \frac{-2 \pm \sqrt{4-4 \cdot (-0.5) \cdot (-3) }}{-1}=\frac{-2 \pm \sqrt{-2}}{-1}\) |
| Nullstellen: | Die
Diskriminante \(D=b^2-4ac\) der Lösungsformel ist negativ.
Die Gleichung hat daher keine Lösung und die vorliegende Funktion hat also keine Nullstelle! |
| Funktionsgraph: |
|