2.4 Funktionsterme ganzrationaler Funktionen aufstellen

Ist über den Verlauf einer ganzrationalen Funktion (Polynomfunktion) eine ausreichende Anzahl von Bedingungen vorgegeben, so kann ein Gleichungssystem aufgestellt werden, aus dem der Term der Polynomfunktion ermittelt werden kann.

 

Für den Term einer Polynomfunktion vom Grad \(n\) müssen \(n+1\) Koeffizienten bestimmt werden. Es müssen daher ebenso \(n+1\) Bedingungen gegeben sein, um den Funktionsterm eindeutig festzulegen!

  

Vorgehen zur Bestimmung des Funktionsterms

• Setze den Funktionsterm mit den einfachen Koeffizientenvariablen  \(a, b, c,...\)  statt \(a_1, a_2, a_3,...\) an.
• Übersetze jede Bedingung in eine Gleichung.
• Löse das entstandene Gleichungssystem.

 

Spezialfälle:

1. Sind die Nullstellen eines Polynoms n-ten Grades gegeben, so kann unmittelbar die Nullstellenform mit dem noch unbekanntem Leitkoeffizienten angeben werden. Zur Bestimmung des Leitkoeffizienten wird eine weitere Information (Bedinung) zum Verlauf des Graphen benötigt!
   
2. Ist der Scheitel einer Parabel gegeben, führt der Weg über die Scheitelpunktform.

 

Beispiel

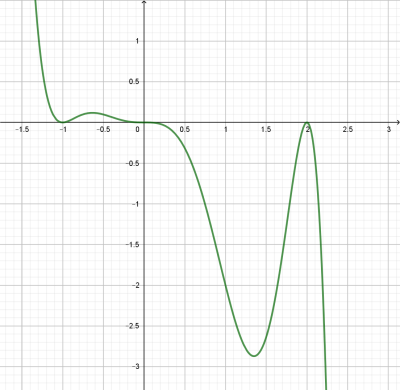
Bestimme zu folgendem Graphen einer Polynomfunktion vom Grad 7 den Funktionsterm.

Die Nullstellen dürfen ganzzahlig abgelesen werden und der Punkt \(P(3 | -216) \) liegt auf dem Graphen \( G_f\).

Aufstellen des Funktionsterms aus den gegebenen ganzzahligen Nullstellen: \(f(x)=a \cdot(x+1)^2 \cdot x^3 \cdot (x-2)^2 \) Es gilt außerdem:   \( \hspace{3cm} f(3)=-216 \) Einsetzen und auflösen nach a:   \( \Rightarrow a \cdot 4^2 \cdot 3^3 \cdot 1^2 = -216 \) \( \Rightarrow a= \frac{1}{2} \) Funktionsterm angeben:   \(\Rightarrow f(x)=\frac{1}{2} \cdot(x+1)^2 \cdot x^3 \cdot (x-2)^2 \)

 

---