2.1 Lineare Funktionen

Die Analyse linearer Funktionen und die Entwicklung eines Funktionsterm aus gegebenen Stücken spielen eine elementare Rolle in vielen Bereichen der Analysis.

 

Grundlegende Eigenschaften

Die Zuordnungsvorschrift einer linearen Funktion lautet: \(\hspace{3mm} f:x \mapsto y=m \cdot x+t \)

• Die Menge der reellen Zahlen \( \mathbb{R} \) bildet die maximale Definitionsmenge.
• Daraus ergibt sich als Wertebereich ebenso die Menge der reellen Zahlen  \( \mathbb{R} \).
• Wir erhalten also eine maximale Zuordnung  \(f: \mathbb{R} \mapsto \mathbb{R}\)
  
  
• t ist der y-Abschnitt bzw. y-Achsenabschnitt der Funktion.
• m ist die Steigung der Funktion bzw. des Graphen der Funktion
   

Allgemeine Bezeichnung:   Die Steigung einer Funktion an einer Stelle \(x_0\) wird in der Mathematik im Allgemeinen als Ableitung \(f'\) an dieser Stelle bezeichnet. Eine Gerade f hat bekanntlich die gleichbleibende (konstante) Steigung m. Daher können wir für alle \(x_0 \in \mathbb D_f\) festhalten: \(m = f'(x_0) \)

 

Schnittpunkte mit den Koordinatenachsen

 

a) Schnittpunkt mit der y-Achse:  \(\hspace{13mm} x=0\)

• Für jede beliebige Funktion erhalten wir für den Wert  \(x=0\) den Schnittpunkt mit der y-Achse.
• Der Graph einer linearen Funktion schneidet die y-Achse somit stets im Punkt \(S_y(0 / t) \)

 

b) Schnittpunkt mit der x-Achse (Nullstelle):  \(\hspace{13mm} f(x)=0\)

• Für jede beliebige Funktion erhalten wir für die zugehörige(n) Nullstelle(n), indem wir den Term der Funktion gleich Null setzen.
• Eine lineare Funktion kann maximal eine Nullstelle aufweisen. Diese erhält man durch Auflösen der entstandenen Gleichung nach der Variablen x.

 

Nullstellenberechnung

 

Allgemeine Gleichung:	Beispiel:
\(f(x)=m \cdot x+t\) Allgemeiner Ansatz: \(f(x_0)=0\) \(m \cdot x_0+t=0\)     | -t \(m \cdot x_0=-t\)         | : m \(x_0 = \frac{-t}{m} \) Schnittpunkt mit der x-Achse: \( N( 0  |  \frac{-t}{m}) \)	\(f(x)=3x+4\) \(3x_0+4=0\)     | -4 \(3x_0=-4\)         | : 3 \(x_0 = \frac{-4}{3} \) \( N( 0  |  \frac{-4}{3}) \)

 

Anmerkung zur Art von Nullstellen:
Eine lineare Funktion kann maximal eine Nullstelle aufweise. Liegt eine Nullstelle vor, so spricht man auch von einer einfachen Nullstelle. Alle Funktionsgraphen schneiden an einfachen Nullstellen die x-Achse, d.h. die y-Werte der Punkte auf dem Funktionsgraphen wechseln an dieser Stelle ihr Vorzeichen.

Grundsätzlich gilt:

Einfache Nullstelle \(x_0\)   \(\Leftrightarrow\)    Nullstelle mit Vorzeichenwechsel

 

Analyse der Steigung des Graphen einer Funktion

  

Die Betrachtung und Beschreibung der Steigung bzw. Steigungsänderung einer Funktion wird im Allgemeinen mit dem Begriff Monotoniebetrachtung angesprochen.

Grundsätzlich kennt man für lineare Funktionen \(f\) folgende Zusammenhänge für den Verlauf eines Graphen \(G_f\) bei vorgegebener Steigung \(m\):

• \(m>0: \)          \(G_f\) ist streng monoton steigend (kurz: s.m.s)
• \(m<0: \)          \(G_f\) ist streng monoton fallend (kurz: s.m.f)
  
  
• \(m=0: \)          \(G_f\) verläuft parallel zur x-Achse

 

Graphen sind streng monoton steigend	Graphen sind streng monoton fallend
Abb. 1: Lineare Funktionen

  

Vergleich mit den jeweiligen Grundfunktionen

  

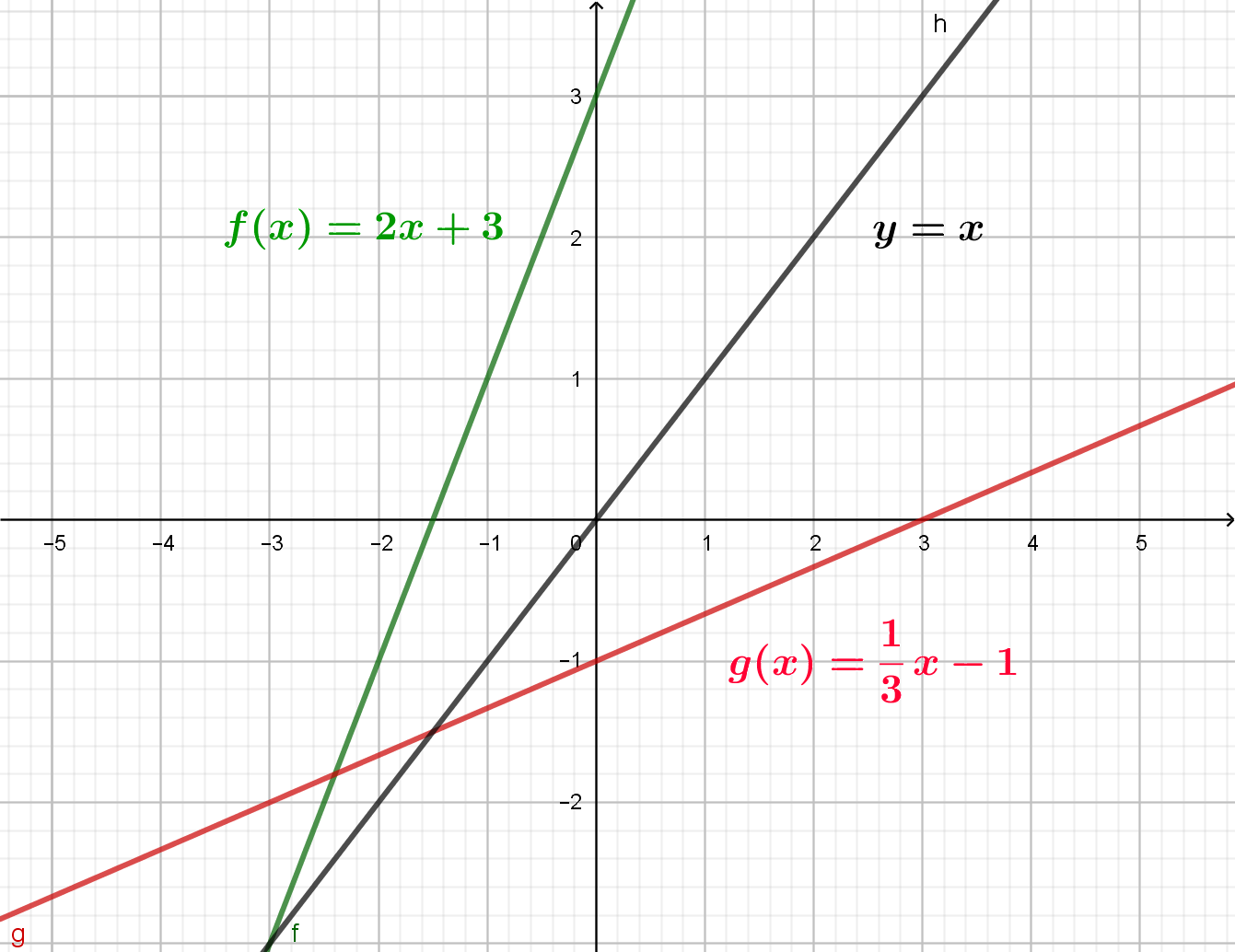
Aus den beiden Grundfunktionen \(y=x\) und \(y=-x\) lassen sich alle lineare Funktionen entwickeln bzw. die speziellen Verläufe damit vergleichen. 

Steigende lineare Funktionen:  m > 0

• \(m>1\)  \(\Rightarrow\)  \(G_f\) verläuft steiler als die Grundfunktion \(y=x\)
• \(m<1\)  \(\Rightarrow\)  \(G_f\) verläuft flacher als die Grundfunktion \(y=x\)

 

Fallende lineare Funktionen:  m < 0

• \(m<-1\)  \(\Rightarrow\)  \(G_f\) verläuft steiler als die Grundfunktion \(y=-x\)
• \(m>-1\)  \(\Rightarrow\)  \(G_f\) verläuft flacher als die Grundfunktion \(y=-x\)

 

---

Funktionsentwicklung an einem Beispiel

Betrachtet wird dazu die Funktion \(h(x)=-2x+1\) aus Abb. 1.

• Der y-Abschnitt \(t=1\) zeigt, dass \(G_h\) um eine Einheit in y-Richtung gegenüber der Grundfunktion \(y=-x\) verschoben wurde.
• Es gilt \(m=-2<-1\), d.h. die Steigung von \(G_h\) ist kleiner als die Steigung der Grundfunktion \(y=-x\).
•  \(G_h\) fällt also steiler als die Grundfunktion \(y=-x\).

 

Die Steigung m als Streckungsfaktor
Der Betrag des Faktors vor der Variablen x ( also der Betrag der Steigung |m|) bewirkt eine Streckung bzw. Stauchung des Funktionsgraphen in y-Richtung gegenüber der jeweiligen Basisfunktion.

 

 

---

Funktionsentwicklung mit zugehörigen Graphen:

Entwicklung des Graphen der Funktion \(G_g\) mit \(g(x)=\frac{1}{3}x-1\) aus der Funktion \(y=x\).

  

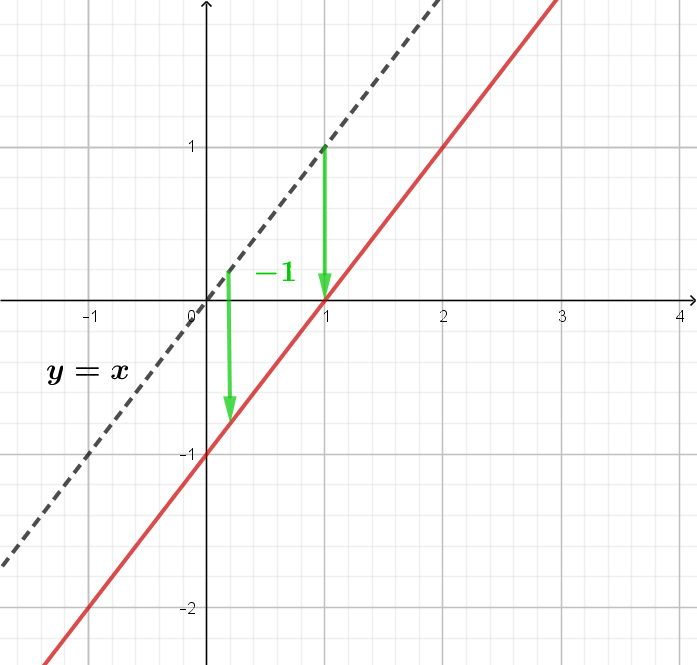	Schritt 1: Der Graph der Funktion \(y=x\) wird um eine Einheit in negativer y-Richung verschoben. D.h. im ersten Schritt werden alle y-Werte der Basisfunktion um 1 verringert. Wir erhalten die Funktionsgleichung \(y=x-1\).
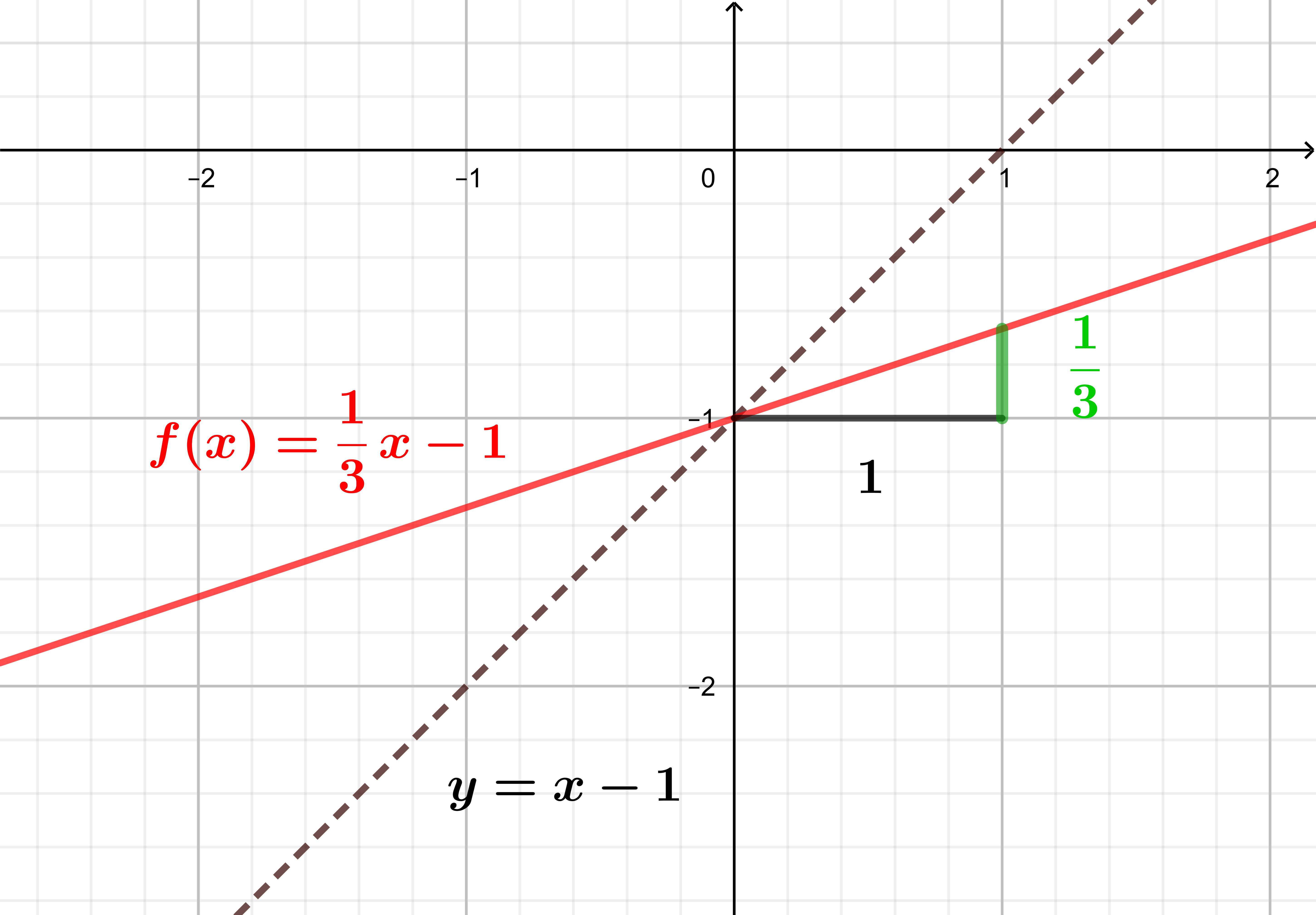	Schritt 2: Ausgehend von Schnittpunkt \(S_y(0 | -1) \)  des Graphen mit der y-Achse wird die neue Steigung \( \frac{1}{3} \) berücksichtigt. Betrachte dazu das eingezeichnete Steigungsdreieck. Der Graph wird im Vergleich zur Funktion \(y=x-1\) mit dem Faktor \(\frac{1}{3} \) gestaucht.

 

---