

Die binomischen Formeln können wir entweder durch einfaches Ausmultiplizieren von Klammern, die aus Binomen bestehen, herleiten oder durch entsprechende geometrische Flächenbetrachtungen begründen.
Analog zu den einführenden Beispielen können wir die binomischen Formeln durch Ausmultiplizieren der jeweiligen Binome herleiten.
Die 1. binomische Formel vereinfacht die Berechnung des Terms: \( ( \color{blue}{a} + \color{red}{b})^2\)
Herleitung durch Ausmultiplizieren:
| Schreibe die Potenz als Produkt | \( ( \color{blue}{a} + \color{red}{b})^2=\) | ||
| Multipliziere jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer. | \( ( \color{blue}{a} + \color{red}{b}) \cdot ( \color{blue}{a} + \color{red}{b})=\) | ||
| Fasse gleichartige Terme zusammen. | \( \color{blue}{a} \cdot \color{blue}{a}+ \color{blue}{a} \cdot \color{red}{b}+\color{red}{b} \cdot \color{blue}{a}+\color{red}{b} \cdot \color{red}{b}=\) | ||
| \(\color{blue}{a^2}+2\color{blue}{a}\color{red}{b}+\color{red}{b^2} \) |
| Wir erhalten die 1. Binomische Formel: \[ (a+b)^2=a^2+2ab+b^2 \] |
Pepe zieht in seine neue Studentenwohnung mit quadratischem Grundriss ein.
| Aus dem Grundriss der Wohnung erkennen wir, dass eine Seite seiner gesamten Wohnung die Gesamtlänge \((a+b)\) hat. |
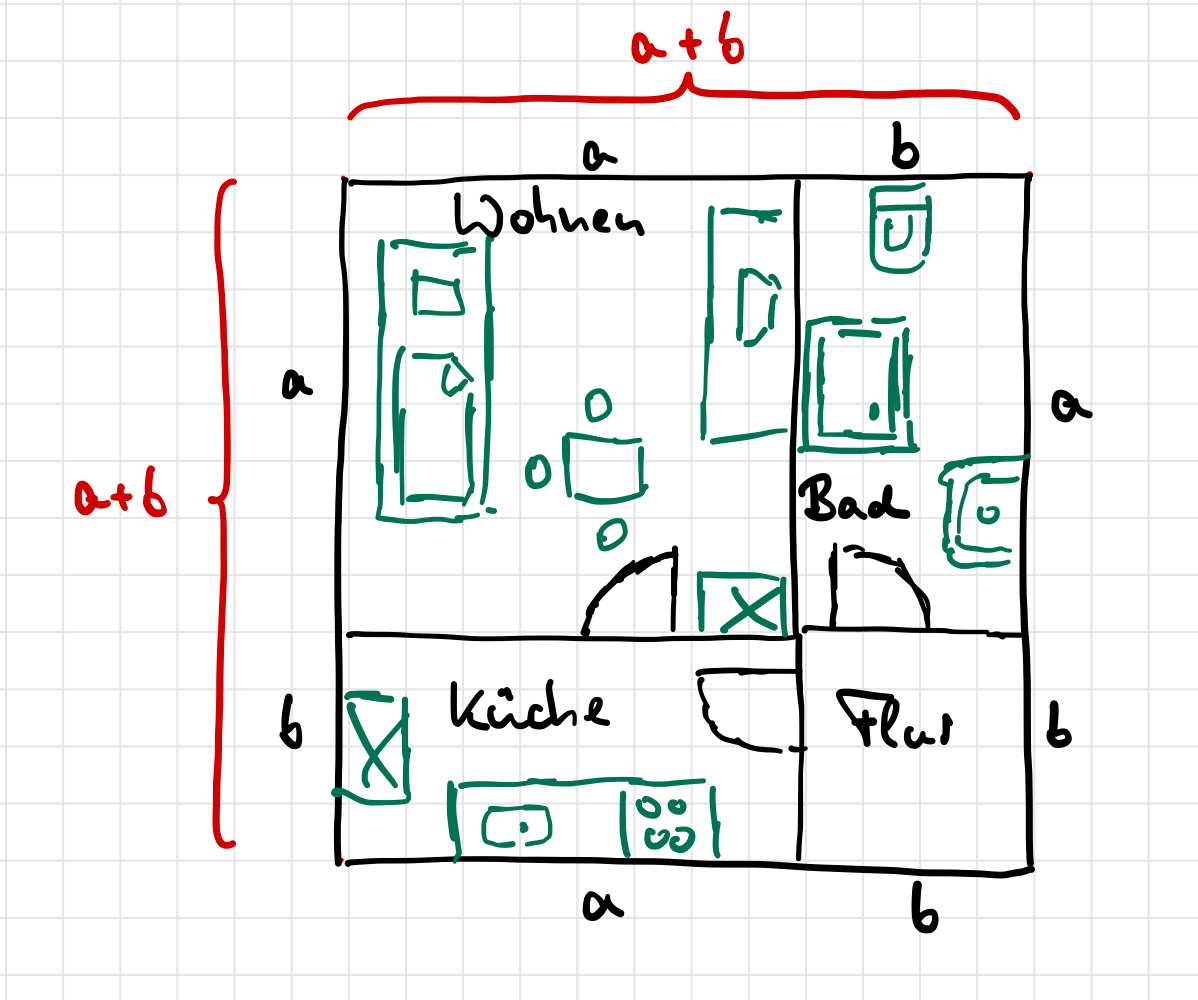 |
| Die Gesamtfläche seiner Wohnung kann er mit den Angaben auf zwei Arten berechnen: | |
|
\(A_{gesamt} \) |
\(= A_{Wohnen} + A_{Küche} + A_{Bad}+A_{Flur} \) |
| \( (a+b) \cdot (a+b)\) | \(= a \cdot a + a \cdot b + b \cdot a+ b \cdot b \) |
| \( (a+b)^2 \) | \(= a \cdot a + a \cdot b + a \cdot b+ b \cdot b \) |
| \(= a^2 + 2ab + b^2 \) | |