9.3 Berechnung der Irrtumswahrscheinlichkeiten

Bei der Entscheidung für die Hypothese \(\small H_0\) oder für die
Gegenhypothese \( \small H_1\) durch einen Hypothesentest treffen wir natürlich aufgrund des Zufalls-Charakters durch den unsere Stichprobe ausgewählt wird, teilweise falsche Entscheidungen, die wir akzeptieren müssen.

 

Fehleranalyse

Nachfolgende Tabelle gibt eine gute Übersicht über unsere möglichen Entscheidungen:

Realität	Entscheidung aufgrund der Stichprobe
	für \(H_0\) mit \(A_0=\{0, 1, 2\}\)	für \(H_1\) mit \(A_1=\{3, 4, 5, ...,10\}\)
\(H_0:p_0=0,15\)	Richtige Entscheidung	Falsche Entscheidung
\(H_1:p_1=0,4\)	Falsche Entscheidung	Richtige Entscheidung

 

Bei der Berechnung der jeweiligen Wahrscheinlichkeiten für unsere möglichen Entscheidungen kommt es selbstverständlich darauf an, welche der Hypothesen in der Realität tatsächlich zutrifft.

Die Berechnung der Wahrscheinlichkeiten für die "Richtigen Entscheidungen" sowie der "Falschen Entscheidungen" erfolgt stets mit Hilfe der entsprechenden kumulativen Verteilungsfunktionen.

---

Irrtümliche Entscheidung für \(\small H_1\)

• Es liegt eine Lieferung der Qualität A vor, was wir bekanntlich nicht sicher wissen.
• D.h. es gilt \(\small H_0: p_0=0,15\)
• Die Stichprobe liefert mehr als 2 Ausschussstücke, z.B. 5.
• Man entscheidet sich fälschlicherweise für \(\small H_1\)

Richtige Entscheidung: \(\small P^{10}_{0,15}(Z\leq 2)= F^{10}_{0,15}(2)=0,82020\) Irrtümliche Entscheidung: \(\small P^{10}_{0,15}(Z>2)= 1-F^{10}_{0,15}(2)=0,1798\)

---

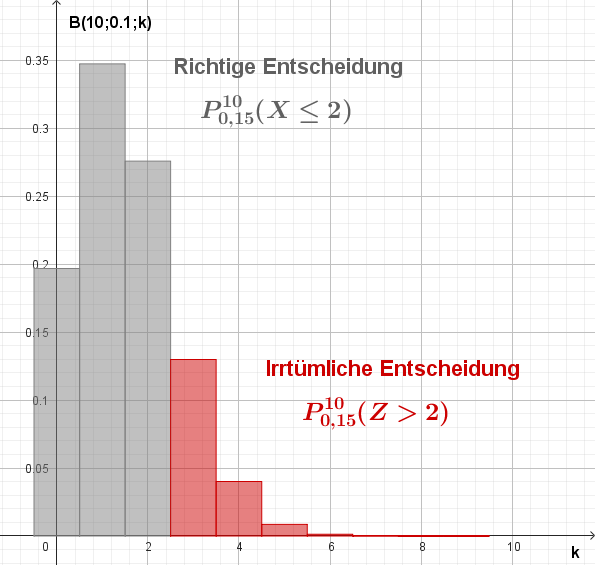Irrtümliche Entscheidung für \(\small H_o\)

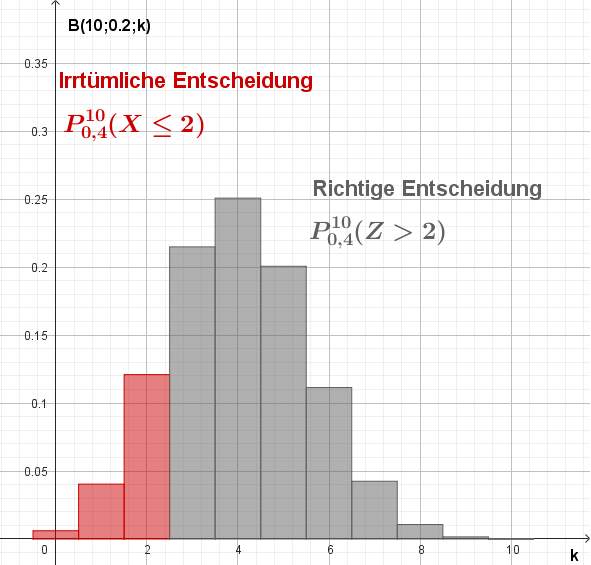• Es liegt eine Lieferung der Qualität B vor, was wir bekanntlich nicht sicher wissen.
• D.h. es gilt \(\small H_1: p_1=0,4\)
• Die Stichprobe liefert höchstens 2 Ausschussstücke, z.B. 1.
• Man entscheidet sich fälschlicherweise für \(\small H_0\)

  

Richtige Entscheidung: \(\small P^{10}_{0,4}(Z>2)= 1-F^{10}_{0,4}(2)=0,83271\) Falsche Entscheidung: \(\small P^{10}_{0,4}(Z\leq 2)= F^{10}_{0,4}(2)=0,16729\)

 

---