7.2 Varianz einer Zufallsgröße

Der Erwartungswert eignet sich nur bedingt für eine umfassende Charakterisierung einer Zufallsgröße.  Trotz der unterschiedlichen Streuungen bei Zufallsgrößen mit ihren jeweiligen Wahrscheinlichkeitsverteilung kann es vorkommen, das die Zufallsgrößen den gleichen Erwartungswert haben.

 

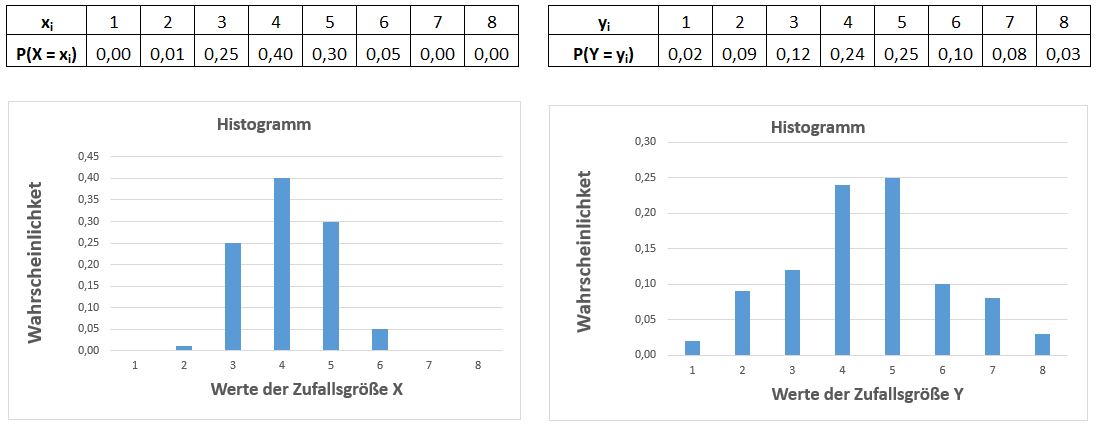
Die Zufallsgrößen \(\small X\)  und \(\small Y\) haben trotz unterschiedlicher Verteilung und Streuung den gleichen Erwartungswert  \(\small E(X)=E(Y)=4,17\).

 

Varianz als Maß der Streuung

Das gebräuchlichste Maß für die Beurteilung der Streuung einer Zufallsgröße \( \small X\) mit ihren Werten \( \small x_i\) und ihren Wahrscheinlichkeiten \( \small P(X=x_i) \) ist die mittlere quadratische Abweichung, auch als Varianz \( \small Var(X)\) bezeichnet:
 

\(\small Var(X)\)	\(\small =  \sum\limits_{i=1}^{n} (x_i- \mu)^2 \cdot P(X=x_i)\)
	\(\small = (x_1- \mu)^2 \cdot P(X=x_1)+ (x_2- \mu)^2 \cdot P(X=x_2)+ ... +  (x_n- \mu)^2 \cdot P(X=x_n) \)

 

• Die Differenz  \(\small (x_i-\mu )\)  berechnet zunächst für jeden Wert der Zufallsgröße den jeweiligen Abstand zum Erwartungswert.
• Warum berechnen wir den Abstand zum Quadrat, also  \( \small (x_i- \mu)^2 \) 
  \(\hspace{3mm}\)- Die Ergebnisse der quadratischen Differenz sind stets positiv.
  \(\hspace{3mm}\)- Es ist daher nicht wichtig, ob das jeweilige \( \small x_i\) kleiner oder größer als \(\mu\) ist.
  \(\hspace{3mm}\)- Eine kleinere Streuung kommt deutlicher zur Geltung.
   
• Die Multiplikation jeder „quadratischen Differenz“ mit \( \small P(X=x_i)\) ergibt die mittlere quadratische Abweichung, der sogenannten Varianz als quantitatives Maß für die Abweichung der Werte einer Zufallsgröße vom Erwartungswert.
• Eine große Varianz bedeutet dabei, dass große Abweichungen der Zufallsgröße X vom Erwartungswert sehr wahrscheinlich sind und umgekehrt ist bei kleiner Varianz eine große Abweichung der Zufallsgröße X vom Erwartungswert sehr unwahrscheinlich sind!

 

 

---