5.5 Extremstellen
Betrachten wir eine Gebirgskette genauer. Wir erkennen neben dem höchsten Gipfel der Zugspitze mehrere etwas niedrigere Gipfel, wie z.B, die Alpspitze, das Kreuzeck, die Dreitorspitze und den Teufelstättkopf.

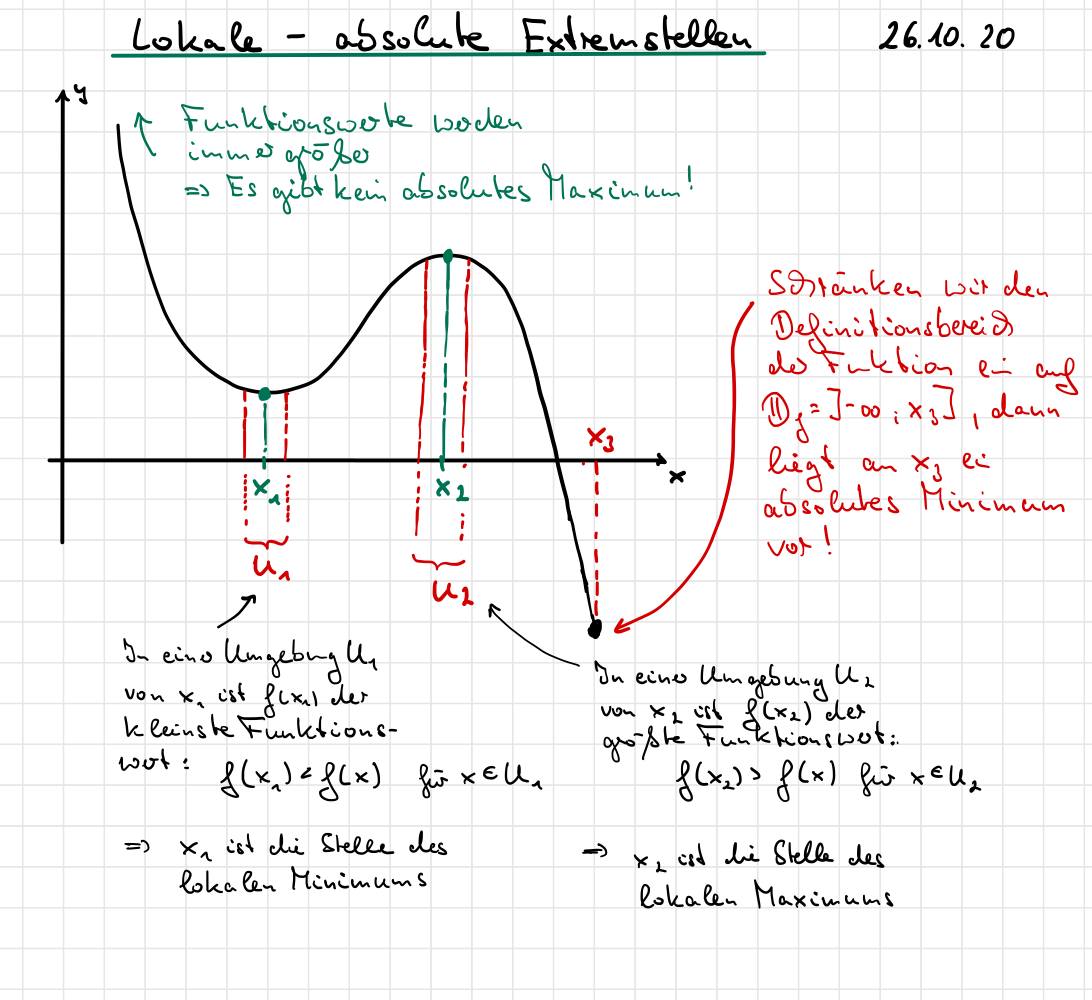
Jeder Gipfel für sich, stellt in seiner nächsten Umgebung den lokal höchsten Punkt (lokales Maximum) dar. Im betrachteten Bereich wäre die Zugspitze der absolut höchste Punkt (absolutes Maximum).
Diese anschauliche Überlegung müssen wir auch auf unsere Erkenntnisse der Kurvendiskussion übertragen. In der Regel stellen unsere Extremstellen mathematisch gesehen ebenfalls lokale Extremstellen dar, die wie folgt definiert werden:
Eine reelle Funktion \(f(x)\) hat an einer Stelle \(x_0\) mit
\(x_0 \in D_f\) ein
|
|
Ergebnisse aus dem Unterricht
Bestimmung der Lage und Art von Extremstellen
- Wenn eine differenzierbare Funktion \(f\) an einer Stelle \(x_0\)
ein lokales Extremum hat, dann gilt immer
\(f'(x_0)=0\).
D.h. wir starten die Bestimmung der lokalen Extremstellen mit der Berechnung der Nullstellen der Ableitungsfunktion.
- Wechselt die Ableitungsfunktion an
der Stelle \(x_0\) ihr Vorzeichen, dann besitzt der
Funktionsgraph \(G_f\) an der Stelle \(x_0\) ein
Maximum oder ein
Minimum.
Betrachten wir die Vorzeichen der Ableitung indem wir auf der x-Achse von links nach rechts gehen, dann gilt:
Vorzeichenwechsel von \(-\) nach \(+\) \( \Leftrightarrow\) ein lokales Minimum liegt vor
Vorzeichenwechsel von \(+\) nach \(-\) \( \Leftrightarrow\) ein lokales Maximum liegt vor
Terrassenpunkt
Wenn die Ableitung einer differenzierbare Funktion \(f\) an einer Stelle \(x_0\) eine Nullstelle hat, d.h. es gilt: \(f'(x_0)=0\).
Die Ableitungsfunktion wechselt aber an der Stelle \(x_0\) ihr Vorzeichen nicht, dann besitzt der Funktionsgraph \(G_f\) an der Stelle \(x_0\) einen sogenannten Terrassenpunkt.
Das grundlegende Monotonieverhalten einer Funktion ändert sich am Terrassenpunkt nicht. Das Vorzeichen der Steigung bleibt also in seiner Umgebung unverändert.
