5.4 Funktion und Ableitungsfunktion
Aus den bisherigen Überlegungen in diesem Kapitel ist bereits deutlich geworden, dass zwischen einer beliebigen Funktion \(f\) und ihrer Ableitungsfunktion \(f'\) wichtige Zusammenhänge bestehen.
Zusammenhänge von Funktion und Ableitung
Die Analyse der Ableitungsfunktion \(f'\) erlaubt einerseits eindeutige Rückschlüsse auf das Steigungsverhalten des Graphen der Funktion \(f\) und andererseits liefern diese Ergebnisse unmittelbar die Lage von Hochpunkten (MAX/HOP), Tiefpunkten (MIN/TIP) und Terrassenpunkten (TP).
| Verlauf des Graphen \(G_f'\) | Vorzeichen der Ableitung | Rückschlüsse auf das Steigungsverhalten von \(G_f\) |
| \(G_{f'}\) verläuft unterhalb der x-Achse |
\(f'(x)<0\) | \(G_f\) fällt streng monoton |
| \(G_{f'}\) hat an \(x_0\) eine Nullstelle | \(f'(x_0)=0\) | \(G_f\) hat an \(x_0\) Steigung 0, d.h. es liegt ein MIN, MAX oder TP vor. |
| \(G_{f'}\) verläuft über der x-Achse |
\(f'(x)>0\) | \(G_f\) steigt streng monoton |
Graphische Analyse der Ableitung
Die Nullstellen der Ableitungsfunktion \(f'\) bestimmen die Monotoniebereiche der Funktion \(f\).
Über die Lage des Graphen \(G_{f'}\) der Ableitung im Koordinatensystem kann das Vorzeichen der Ableitung \(f'\) im jeweiligen Monotonieintervall eindeutig beschrieben werden, wodurch wiederum das Steigungsverhalten des Graphen \(G_f\) angegeben werden kann.
Die graphische Aufbereitung der Zusammenhänge beruht auf
folgenden Funktionstermen:
- \(f(x)=0,03x^4+0,03x^3-0,3x^2\)
- \(f'(x)=0,12x^3+0,09x^2-0,6x\) mit den Nullstellen \(x_1=-3\), \(x_2=0\) und \(x_3=2\)
Festlegung der Monotoniebereiche und Extremstellen
| Grundlegende Zusammenhänge | |
| Das Video klärt grundlegende Zusammenhänge zw. dem Verlauf des Graphen von \(f'(x)\), dem Vorzeichen der Ableitungsfunktion \(f'(x)\) im jeweiligen Monotonieintervall und dem Steigungsverhalten des Graphen \(G_f\). | |
| Graphisch - rechnerische Zusammenhänge | |
| Das Video verbindet die Betrachgung des Vorzeichens der Ableitung mit dem Verlauf des Graphen von \(f'(x)\). | |
| Entwicklung der Skizze des Graphen aus der Monotoniebetrachtung | |
|
Entwicklung der Skizze eines Graphen für eine Polynomfunktion. Die Ableitungsfunktion hat lauter einfache Nullstellen. |
|
| Entwicklung der Skizze des Graphen aus der Monotoniebetrachtung | |
|
Entwicklung der Skizze eines Graphen für eine Polynomfunktion. Die Ableitungsfunktion hat eine doppelte Nullstellen. |
|
Übung:
Gegeben ist die Funktion \(f(x)=x^4-4x^2\) mit
ihrem Definitionsbereich \(D_f=R\).
Untersuche die Funktion auf:
- Nullstellen
- Verhalten im Unendlichen
- Monotonieverhalten mit Extremstellen
Lösungen: Notwendige Berechnungen

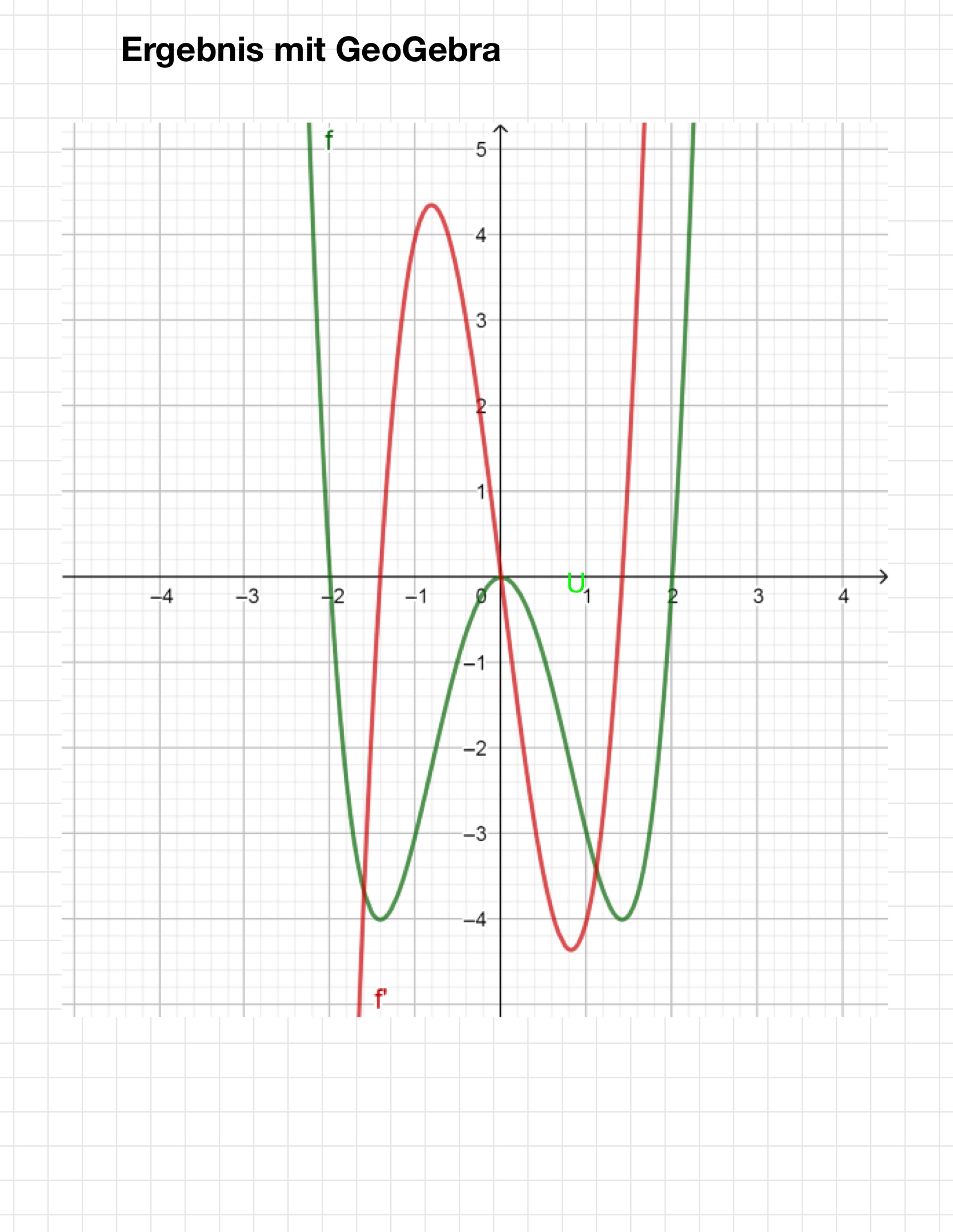
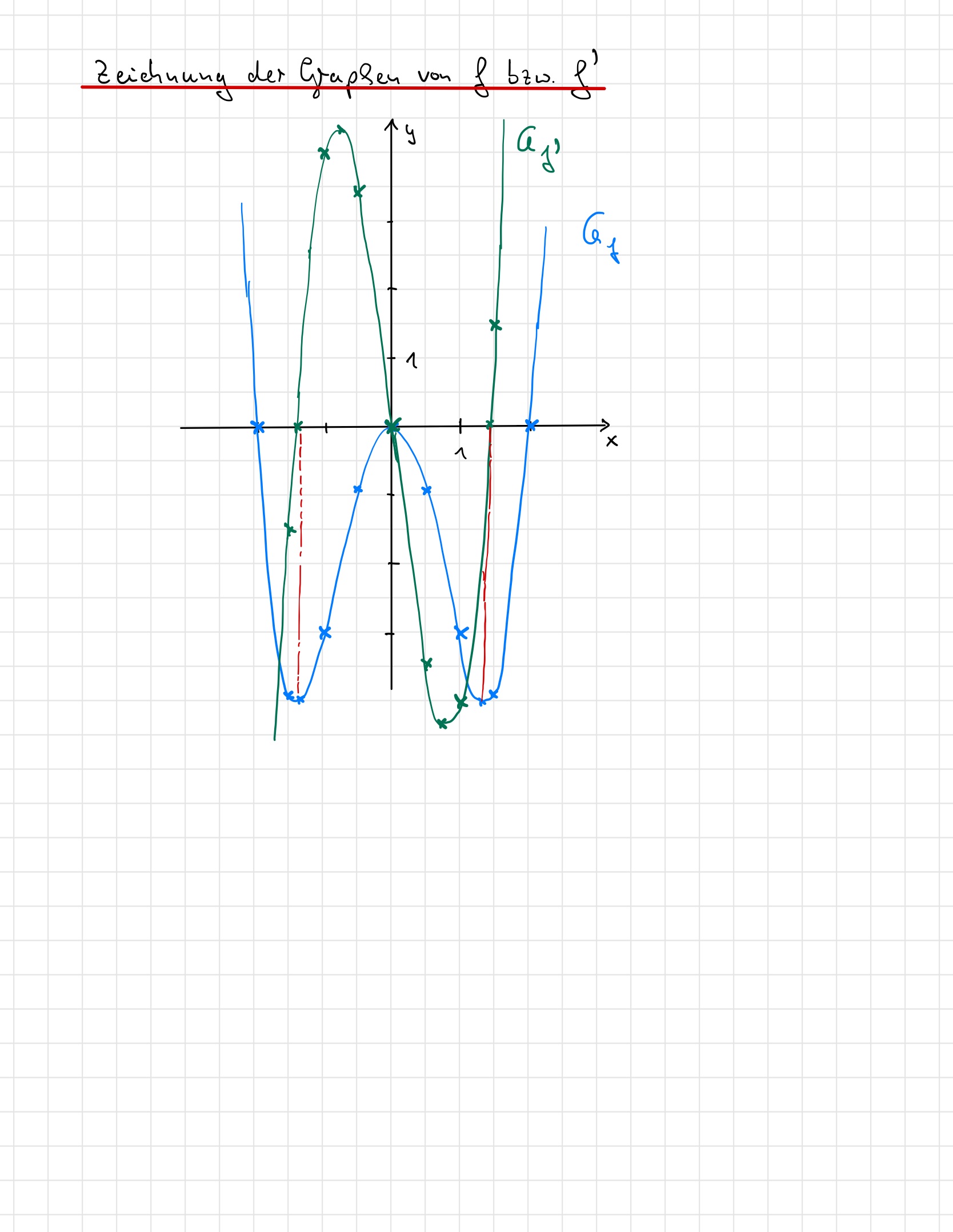
Lösungen: "Freihand" - Zeichnung
Lösungen: Geogebra - Zeichnung