5.1 Unterschiedliche Typen der Monotonie von Funktionen
Hinsichtlich des Steigungsverhaltens unterscheidet man vier Typen, die durch folgende Beispiele veranschaulicht werden. Die strenge Monotonie schließt waagerechte Bereiche einer Funktion aus. Sie verlangt, dass eine Funktion stets steigt oder fällt und ist damit eine stärkere Eigenschaft als die Monotonie.
Für jede differenzierbare (ableitbare) Funktion \(f\) wird die Art der Monotonie mit dem Vorzeichen der Ableitung \(f'\) charakterisiert.
Streng monotone Funktionen
|
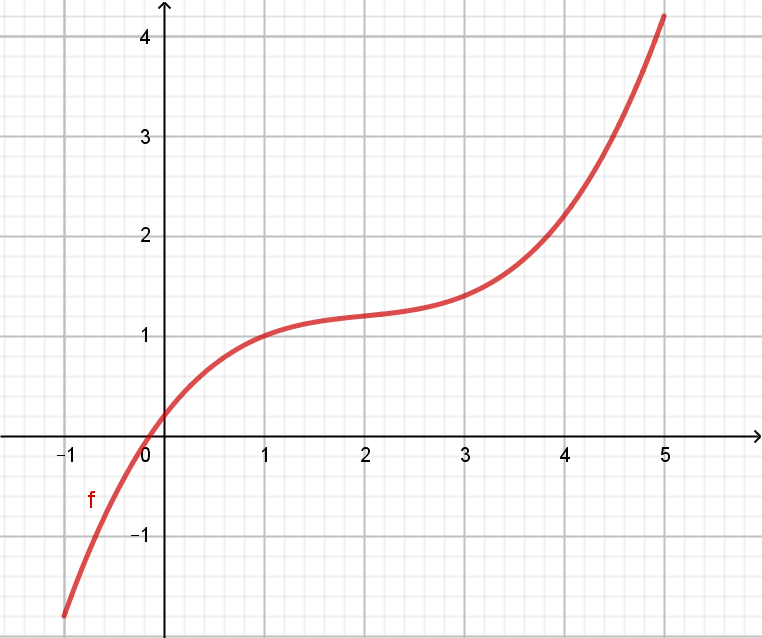
streng monoton steigende Funktion \(f'(x)>0 \Leftrightarrow f \) ist streng monoton steigend |
streng monoton fallende Funktion \(f'(x)<0 \Leftrightarrow f \) ist streng monoton fallend |
 |
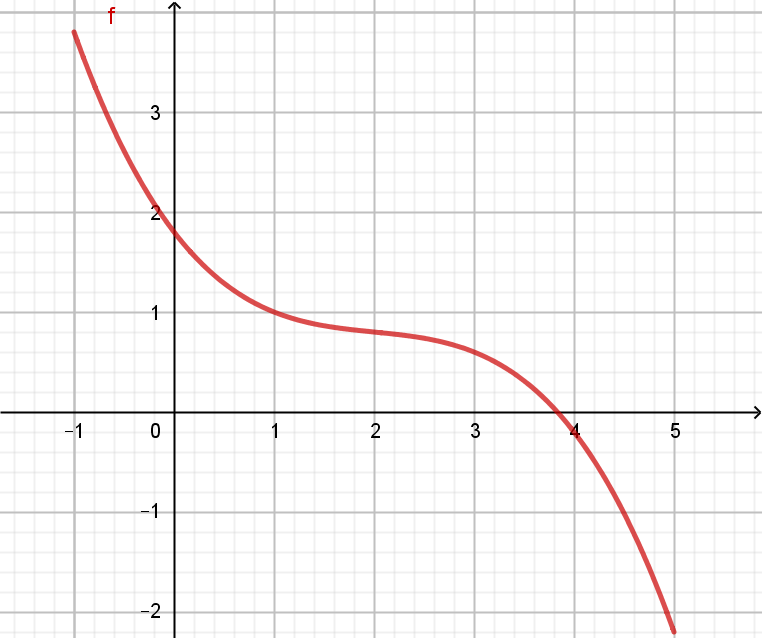 |
| Beide Funktionsgraphen steigen bzw. fallen im gesamten Bereich. Es gibt keine waagrechten Anteile im betrachteten Intervall. D.h. beide Funktionen steigen bzw. fallen streng monoton. | |
Monotone Funktionen
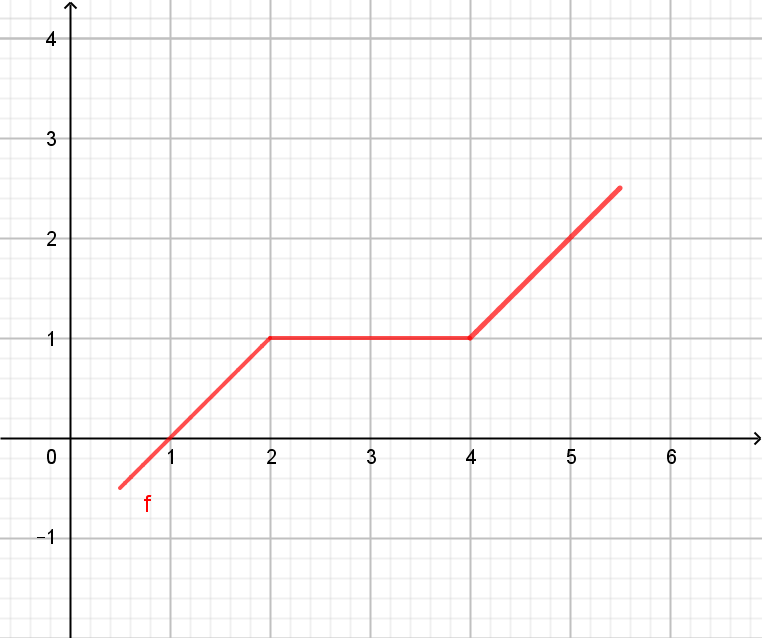
monoton steigende Funktion \(f'(x) \geq 0 \Leftrightarrow f \) ist monoton steigend |
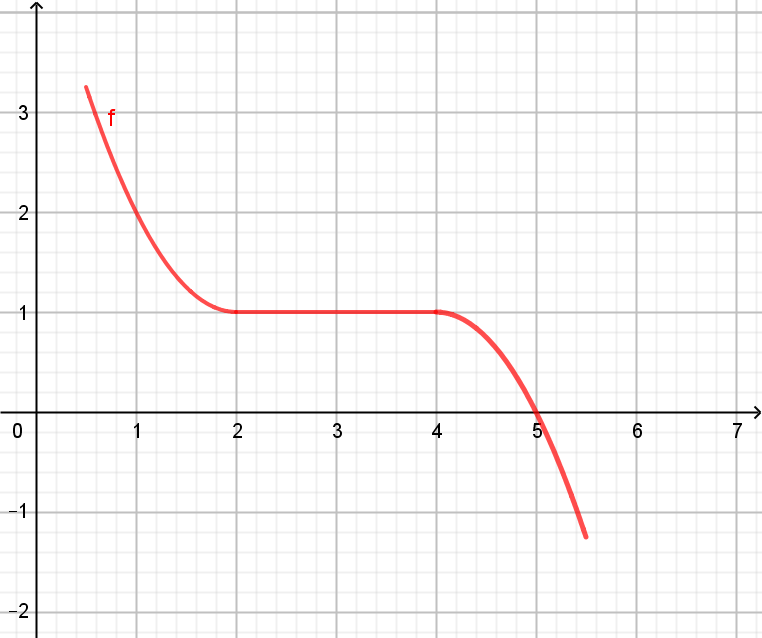
monoton fallende Funktion \(f'(x) \leq 0 \Leftrightarrow f \) ist monoton fallend |
 |
 |
|
In beiden Funktionsgraphen gibt es waagrechte Anteile. Im betrachteten Intervall ändert sich die Monotonie grundsätzlich jedoch nicht.
|
|
