Bild oben

4.6 Graphen gebrochen rationaler Funktionen und deren Asymptoten

  • Aus den vergangen Lerneinheiten ist bekannt, dass die senkrechte Asymptoten durch die Lage der Definitionslücken einer Funktion festgelegt werden.
  • Die waagerechte Asymptote ergibt sich durch die Funktionswerte, die sich für sehr große und sehr kleine x-Werte ergeben.

Beispiel:

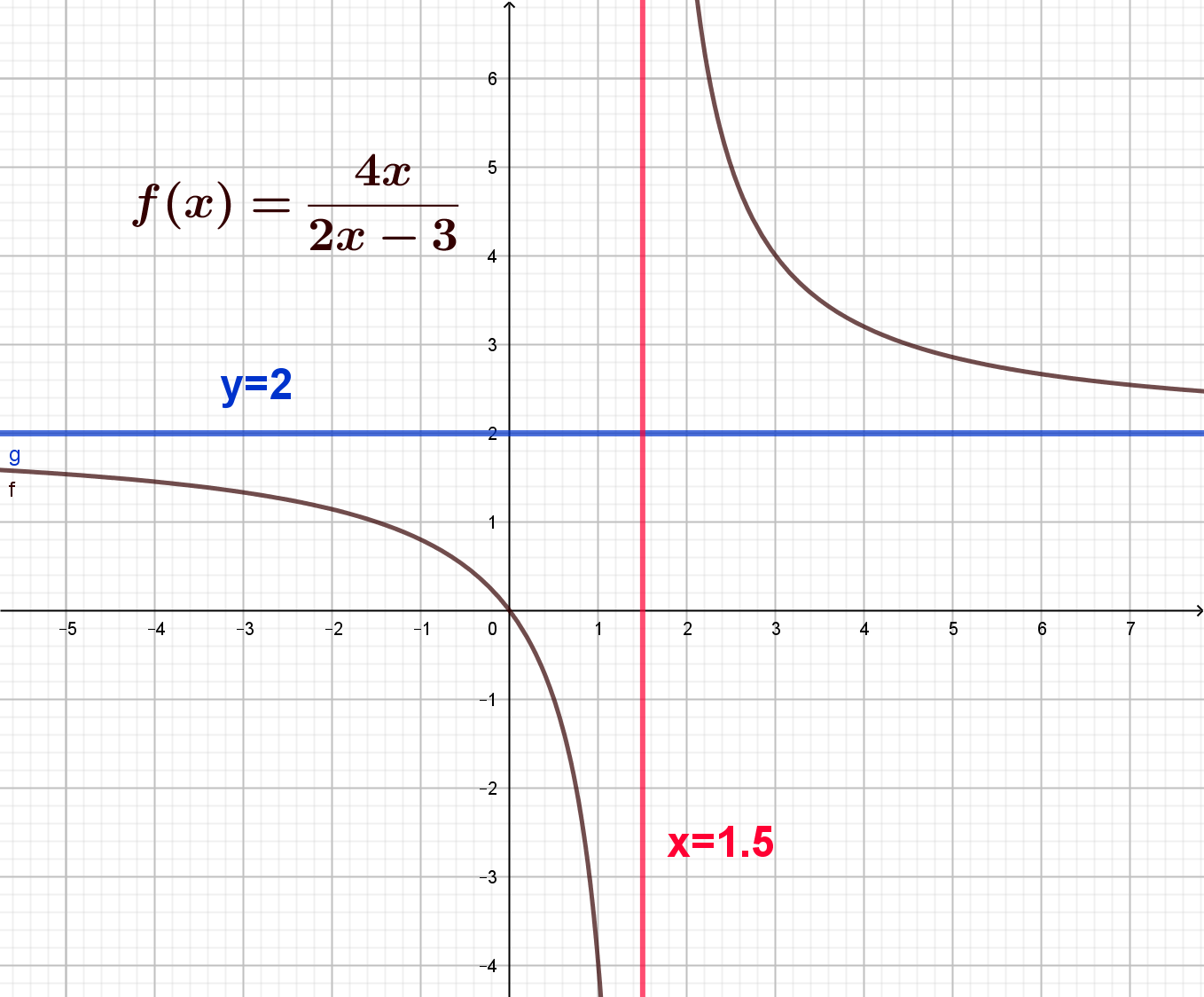
Betrachten wir den Graphen der Funktion

 \(f(x)=  \frac{4x}{2x-3} \)

Der Nenner ist für \(x=1,5 \) null und wir erhalten daher die Definitionsmenge
\(D_f=Q \setminus \{ 1,5 \} \) , was uns wieder zur senkrechten Asymptote \(x=1,5\) bringt.

Ungewöhnlich ist für uns die waagerechte Asymptote  \(y=2\).

Setzt in die Funktion mehrere sehr große und mehrere sehr kleine x-Werte ein und ihr werdet diese waagrechte Asymptote bestätigen können.		   gebr_rat_Fkt

Berechnet beispielsweise folgende Funktionswerte: 
\(f(-1000)=...\)  \( f(-100)=...\)  \( f(-10)=...\)  ...  \(f(10)=...\)   \(f(100)=...\)   \(f(1000)=...\)  

 

Zeichnen und analysieren von Funktionsgraphen 

Damit wir noch mehr Routine bei der Bestimmung der Asymptoten bekommen, müssen wir möglichst viele Graphen unterschiedlichster Funktionen zeichnen. Aber wir sind schlau und lassen zeichnen...

Mit dem GeoGebra Grafikrechner online sollte uns das problemlos gelingen.

 

Aber erst die Anleitung lesen:

  •  Mit einem Klick auf die unten dargestellte Grafik "Geogebra Grafikrechner" öffnet sich ein Fenster, in dem du die Graphen beliebiger Funktionen zeichnen kannst.

  • In das Eingabefeld wird der Funktionsterm eingeben:

    4x / 2x-3 mit PC-Tastatur
    4x \( \div{}\)  2x-3 mit Bildschirmtastatur

  • ... und schon wird der Graph gezeichnet.
 GeoGebra 
ACHTUNG: Kommas müssen als Punkte im Funktionsterm geschrieben werden!

GeoGebra

Nach diesen Vorbereitungen sollt ihr mit dem Programm "spielen". Zeichnet möglichst viele Graphen von Funktionen, damit ihr einerseits sicher im Umgang mit Geogebra werdet und andererseits ein Gefühl bekommt, wie so ein Graph ausschauen muss. Unser Buch oder euer Heft gibt viele Beispiele her.

Für Graphen von gebrochen rationalen Funktionen überlegt ihr euch jedes mal zuerst, welche Asymptoten zu erwarten sind und vergleicht Eure Erkenntnisse dann mit dem gezeichneten Graphen!

Pflichtprogramm:

Hausaufgabe: Buch S. 109 / 4, 5

Die Graphen beider Aufgaben nur mit dem Online-Tool zeichnen. Ihr braucht heute nichts schreiben.

In dieser Einheit nur:

  • Asymptoten überlegen - Graph zeichnen - Überlegungen überprüfen
  • Asymptoten überlegen - Graph zeichnen - Überlegungen überprüfen
  • Asymptoten überlegen - Graph zeichnen - Überlegungen überprüfen
  • usw.

 

Übertrage den Hefteintrag in dein Schulheft und erledige die dazugehörige Hausaufgabe!

Hefteintrag Aufgabe Lösung