

Die Auswertung einer Fahrradtour als Beispiel
Wenn du mit deinem Fahrrad eine bestimmte Strecke s
fahren möchtest, dann hängt die Zeit, die du für diese Strecke benötigst, von
deiner Geschwindigkeit ab. Möchtest du beispielsweise mit dem Fahrrad über möglichst viele
Fahrradwege und Nebenstraßen von Hohenfurch nach
Hohenpeißenberg fahren, so beträgt die Strecke etwa 20 km.
Unter der Annahme, dass du mit einer gleichbleibenden Geschwindigkeit \(v \; \frac{km}{h} \) unterwegs bist, kannst du die jeweils benötigte Zeit \(t\) mit der Formel \(t=\frac{s}{v} \) berechnen:
\( \hspace{ 2em} v=8\; \frac{km}{h} \hspace{ 2em} \Longrightarrow \hspace{ 2em} t=\frac{20km}{8 \frac{km}{h}}=2,5 \;h \)
\( \hspace{ 2em} v=10\; \frac{km}{h} \hspace{ 2em} \Longrightarrow \hspace{ 2em} t=\frac{20km}{10 \frac{km}{h}}=2,0 \;h \)
\( \hspace{ 2em} x=15\; \frac{km}{h} \hspace{ 2em} \Longrightarrow \hspace{ 2em} t=\frac{20km}{15 \frac{km}{h}} \approx 1 \;h \;20 \;min \)
\( \hspace{ 2em} v=22\; \frac{km}{h} \hspace{ 2em} \Longrightarrow \hspace{ 2em} t=\frac{20km}{22 \frac{km}{h}} \approx 55 \;min \hspace{ 3em} usw. \)
Du könntest diese Berechnung für unendlich viele denkbare Geschwindigkeiten ausrechnen oder die Mathematik zur weiteren Analyse ins Spiel holen...
|
Für die weitere Untersuchung geben wir der Geschwindigleit die Variable x und der jeweils berechnete y-Wert wäre dann unsere benötigte Zeit. Wir können dann den Zusammenhang zwischen der Geschwindigkeit und der Zeit als Funktion \(f\) betrachten, die jeder Geschwindigkeit \(x\) eine eindeutige Zeit \(y\) zuordnet. \[ f: x \mapsto y = \frac{20}{x} \] |
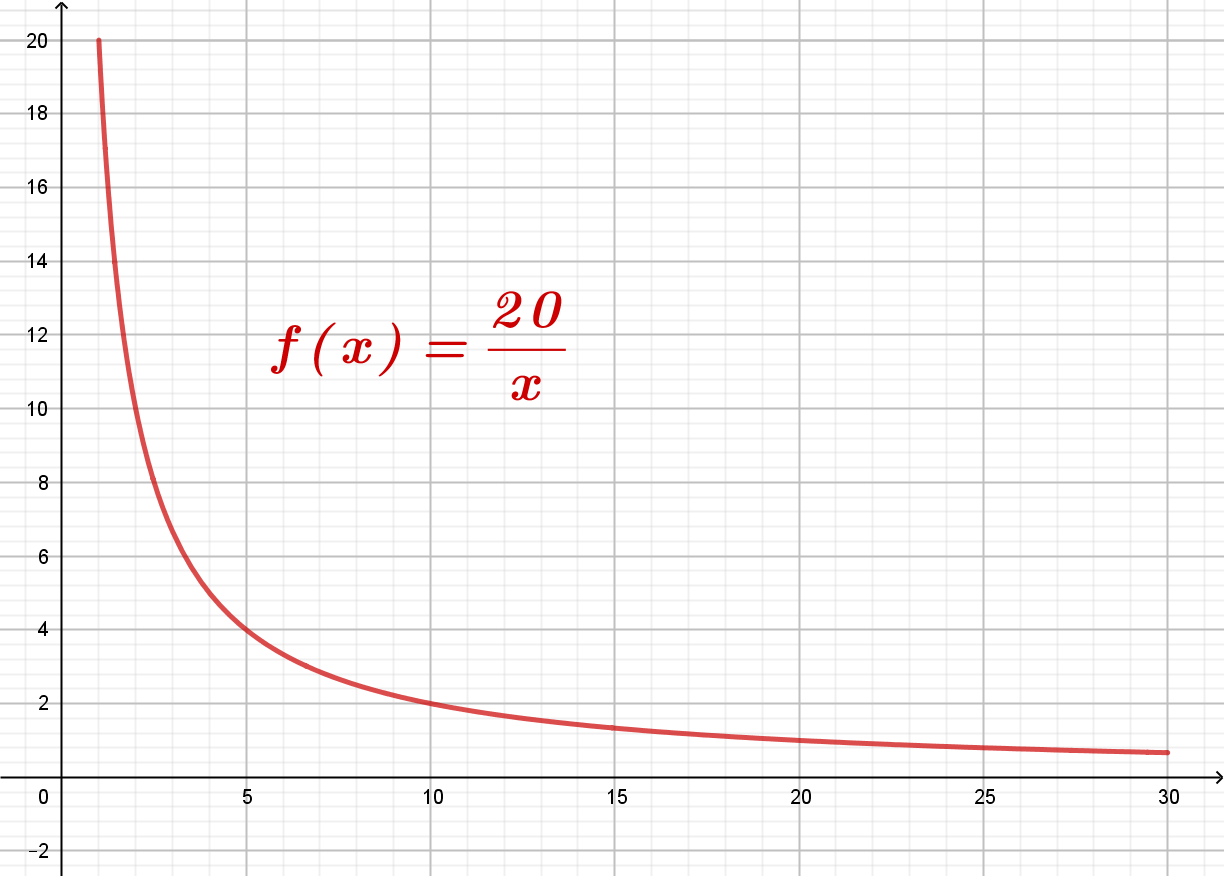 |
Mit Hilfe dieser Funktion \(f\) können wir beliebig viele Punkte berechnen und den Graphen der Funktion zeichnen!
Analyse von Funktionen mit Bruchtermen
Und schon sind wir mitten in der Untersuchung von Funktionen mit Bruchtermen. In der Regel können wir in diese Funktionen auch negative x-Werte einsetzen. Wie üblich suchen wir uns eine ausreichende Anzahl geschicker x-Werte, berechnen die zugehörigen y-Werte und können uns mit Hilfe einer Wertetabelle den Graphen der Funktionen erarbeiten.
Das typische Vorgehen bei Funktionen mit Bruchtermen beschreibt das folgende Video:
Übertrage den Hefteintrag in dein Schulheft und erledige die dazugehörige Hausaufgabe!
| Hefteintrag | Aufgabe | Lösung |