

Funktionen wie \(f:x\mapsto \frac{1}{x}\), \(g:x\mapsto \frac{2}{x+3}\)
oder \(h:x\mapsto \frac{5-t}{t^2}\), deren Funktionsterm ein Bruchterm ist,
heißen gebrochen rationale Funktionen.
Definitionsbereich und Definitionslücken
Alle x-Werte
für die der Nenner null wird, dürfen in den Funktionsterm nicht eingesetzt
werden. Diese Werte können also nicht in der Definitionsmenge enthalten sein.
Beispiel: In die Funktion \(g:x\mapsto \frac{2}{x+3}\) dürfen wir \(x_n = -3 \) nicht einsetzen.
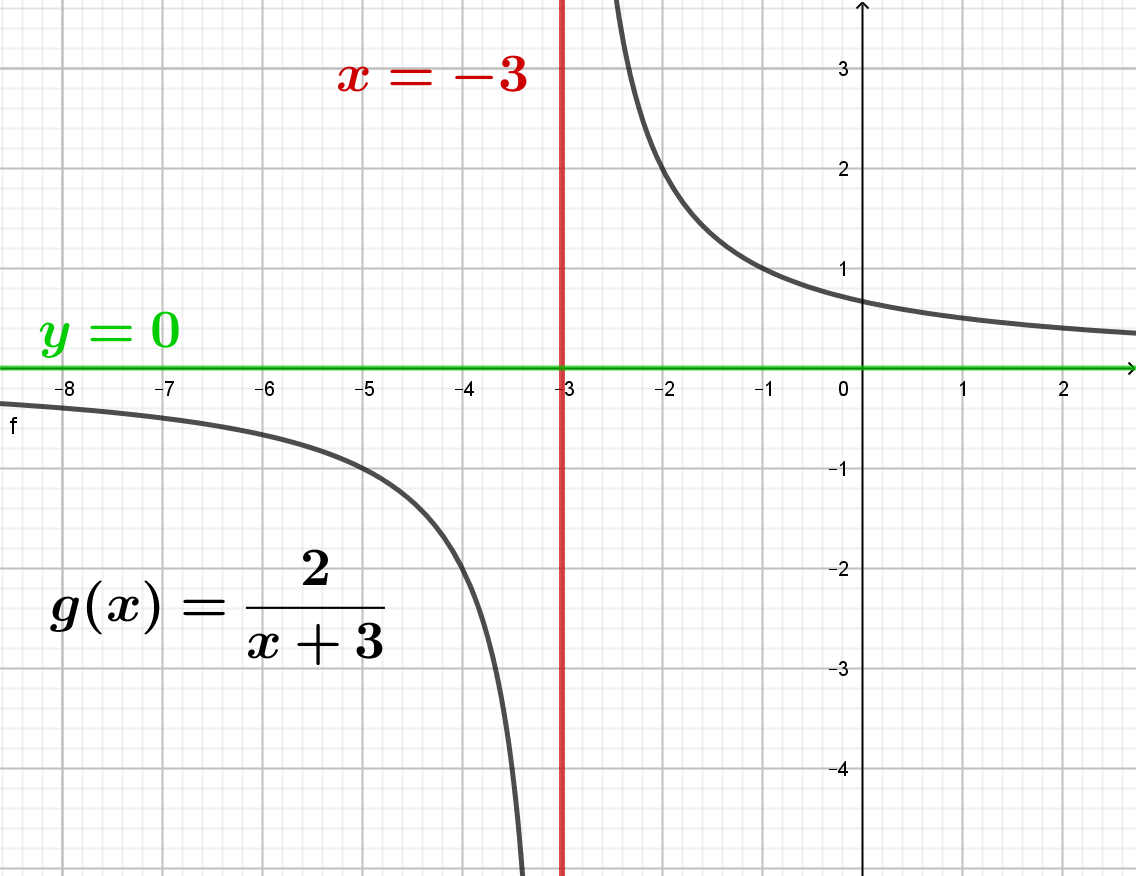 Für
unendlich große (positive) x-Werte und unendlich kleine (negative)
x-Werte nähern sich die Funktionswerte der Zahl 0 an. Der Graph
schmiegt sich an die Gerade \(y=0\) an. Man nennt diese
waagerechte Asymptote
des Graphen von \(f\) . Für
unendlich große (positive) x-Werte und unendlich kleine (negative)
x-Werte nähern sich die Funktionswerte der Zahl 0 an. Der Graph
schmiegt sich an die Gerade \(y=0\) an. Man nennt diese
waagerechte Asymptote
des Graphen von \(f\) .Die senkrechte Gerade \(x=-3\) ergibt sich stets durch die Definitionslücke. Sie ist die senkrechte Asymptote des Graphen, da sich der Graph an diese Gerade für x-Werte nahe an der Definitionslücke annähert. Die Funktionswerte in der Nähe der Definitionslücke werden
unendlich groß bzw. unendlich klein. Das bedeutet, dass der Graph
den gezeichneten Ausschnitt des Koordinatensystems nach oben bzw.
nach unten verlässt! |
Definitonsmenge, Wertetabelle und Graph
|
|
Übertrage den Hefteintrag in dein Schulheft und erledige die dazugehörige Hausaufgabe!
| Hefteintrag | Aufgabe | Lösung |