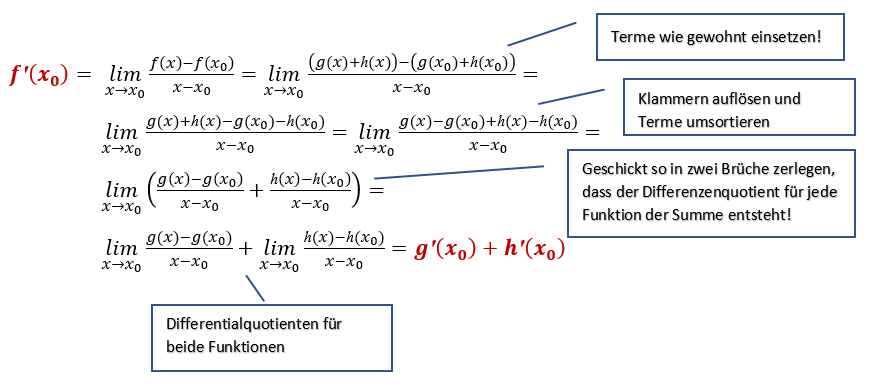
4.3 Die Summenregel
Lässt sich eine Funktion \(f\) darstellen in der Form
\[f(x)=g(x) + h(x)\hspace{3cm} z.B.: \hspace{1cm} f(x)=x^5+ x^3\]
d.h. die Funktion \(f(x)\) ergibt sich durch die Summe der beiden
Funktionen \(g(x)\) und \(h(x)\), dann erhält man durch Berechnung des Differentialquotienten
für ihre Ableitung an einer Stelle \(x_0\) die sogenannte Summenregel:
Ableitung einer Funktion des Typs:
\(f(x)= g(x) + h(x) \)
|
Sind die Funktion \(g\) und \(h\) an der Stelle \(x\)
differenzierbar, d.h. es existiert dort der Grenzwert des
Differentialquotienten, so gilt für die Berechnung der Ableitung
\(f'(x)\) die
Summenregel: \[f(x)=g(x) + h(x) \hspace{1cm} \Longrightarrow \hspace{1cm} f'(x)=g'(x) + h'(x) \] |
Anwendung der Summenregel
