4.2 Die Faktorregel

Lässt sich eine Funktion \(f\) darstellen in der Form

\(f(x)=c \cdot g(x) \hspace{3cm} z.B.: \hspace{1cm} f(x)=5 \cdot x^3\)

d.h. die Funktion \(f(x)\) ergibt sich durch ein Produkt der Funktion \(g(x)\) und einem konstanten Faktor \(c\), dann erhält man für ihre Ableitung an einer Stelle \(x_0\), durch Umformung des Differentialquotienten, die sogenannte Faktorregel:

 

Ableitung einer Funktion des Typs:   \(f(x)=c \cdot g(x)\)

 

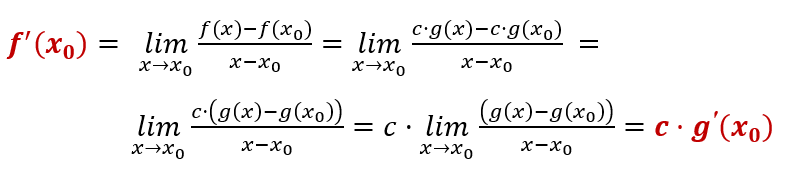
Ist die Funktion \(g\) an der Stelle \(x\) differenzierbar, d.h. es existiert dort der Grenzwert des Differentialquotienten, so gilt für die Berechnung der Ableitung \(f'(x)\) für alle \(c \in R\) die Produktregel:   \[f(x)=c \cdot g(x)  \hspace{1cm} \Longrightarrow  \hspace{1cm} f'(x)=c \cdot g'(x) \]

 

Anwendung der Faktorregel

 

 

---