3.1 Mittlere Änderungsrate

 

Beispiel:
Die nachfolgende Abbildung zeigt eine Näherung der Wertentwicklung eines Fahrzeugs mit einem Neuwert von etwas 20500 €.
 

  

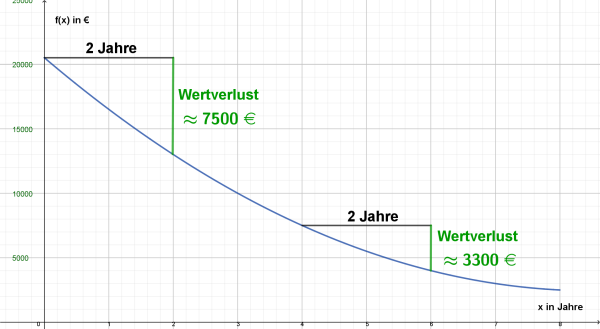
Aus dem Graphen kann absolute Wertänderung für beliebige Zeiträume abgelesen werden.

• Im Zeitraum \([0; 2]\) Jahre:  \(f(2)-f(0) \approx 13000 \space € - 20500 \space € \approx -7500 \space € \)
   
• Im Zeitraum \([4; 6]\) Jahre:  \(f(6)-f(4) \approx 4000 \space € - 7300 \space € \approx -3300 \space € \)

 

Die mittlere Wertänderung (pro Jahr) erhält man, indem man die absolute Wertänderung durch die Länge des jeweiligen Zeitraums teilt:
 

• In den ersten beiden Jahren beträgt die mittlere Wertänderung
   
    \( \frac{13000-20500}{2-0} = \frac{-7500}{2}=-3750, \hspace{3cm} \) also 3750 € Verlust pro Jahr.
   
• Im zweiten Zeitraum beträgt die mittlere Wertänderung
   
    \( \frac{4000-7300}{6-4} = \frac{-3300}{2}=-1650, \hspace{3.3cm} \) also 1650 € Verlust pro Jahr.

 

Zusammenhang mit dem Graphen:
Im zweiten Zeitraum ist der Betrag der mittleren Änderungsrate deutlich geringer, was sich am Graphen durch das erheblich geringere Gefälle bemerkbar macht.

 

Definition Differenzenquotient

Ist die Funktion \(f\)  im Intervall \( [x_0; x_1] \) definiert, so heißt der Quotient    \( \frac{f(x_1)-f(x_0)}{x_1-x_0} \)  die mittlere Änderungsrate der Funktion \(f\) im Intervall \( [x_0; x_1] \).
Dieser Quotient wird auch als Differenzenquotient bezeichnet. Anschaulich entspricht \(m_s= \frac{f(x_1)-f(x_0)}{x_1-x_0} \)   der Steigung der Sekante durch die Punkte \(P(x_0 | f(x_0) \) und   \(Q(x_1 | f(x_1) \) des Graphen der Funktion \(f\).

 

Mittlere Änderungsrate

Video zur Herleitung mit Erklärungen und einem Zahlenbeispiel!
 

 

---