1.2 Darstellungsformen von Funktionen

Grundsätzlich kann eine Funktion dargestellt werden durch

• ihre Zuordnungsvorschrift,
• einer Wertetabelle, die x und die berechneten y-Werte gegenüberstellt
• und einem Funktionsgraphen der sich aus diesen Werten ergibt.

Wie das folgende Beispiel zeigt, muss der Graph einer Funktion keine zusammenhängende "Linie" sein.

Ein "gezinkter" Würfel

Ein Spielbankbetreiber möchte seinen Gewinn maximieren. An einem Spieltisch verwendet er dafür einen "unfairen" Würfel, bei dem die Wahrscheinlichkeiten der einzelnen Seiten unterschiedlich sind. Es handelt sich also um keinen Laplace-Würfel.

Wertetabelle der Funktion	Graph der Funktion
\( \small\omega_i\) 1 2 3 4 5 6 \(P(\small \{\omega_i\})\) 0,1 0,2 0,3 0,15 0,1 0,05

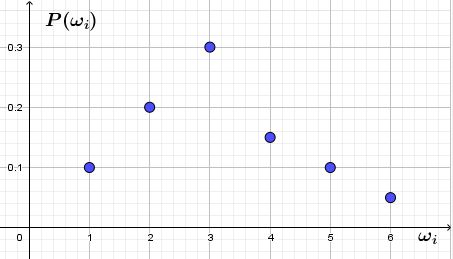• Der Funktionsname ist \(\small P\).
• Die Funktionsvariable ist \(\small \omega_i\) für die Würfelergebnisse
• Mögliche Würfelergebnisse ergeben den Definitionsbereich der Funktion: \(\small D_f= \{1;2;3;4;5;6 \} \)
• Die Wahrscheinlichkeiten der einzelnen Ergebnisse bestimmen den Wertebereich der Funktion: \(\small W_f = \{0,05; \space 0,1; \space 0,15; \space 0,2; \space 0,3 \} \)
• Die Zuordnungsvorschrift lautet in diesem Fall \(\hspace{10mm}  \omega_i \mapsto P(\{\omega_i\})\)