1.1 Der Funktionsbegriff

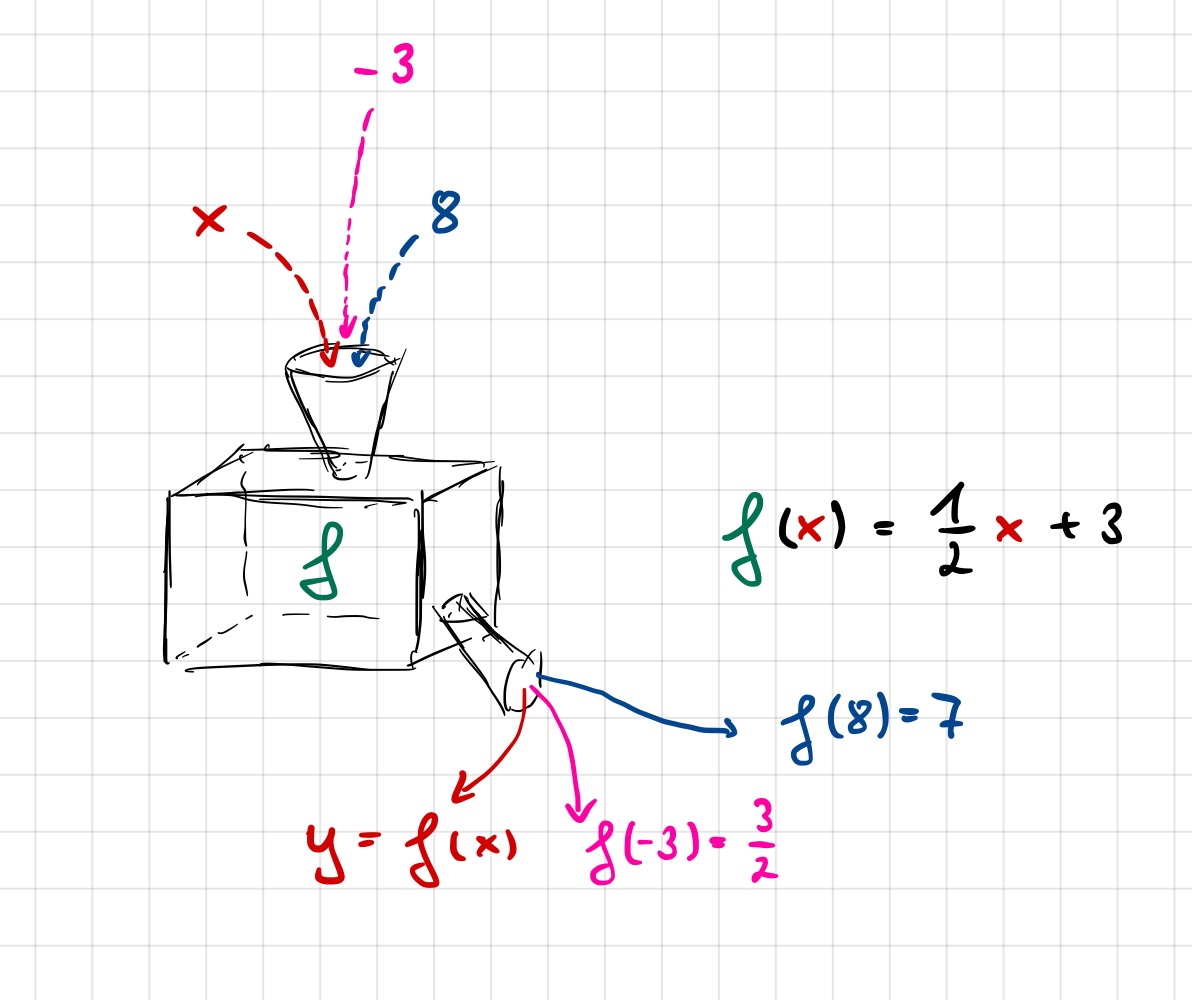
Grundsätzlich verarbeiten Funktionen Eingabewerte, die sie gemäß einem vorgegebenem Funktionsterm eindeutig verarbeiten. Vergleichbar ist eine Funktion mit einer Maschine, die diese Eingabewerte aufnimmt, entsprechend verarbeitet und dann ein eindeutiges Ergebnis ausgibt.

Wir kennen dieses Prinzip auch aus dem Fach Informatik. Dort sprechen wir vom E-V-A-Prinzip, dabei stehen E für Eingabe, V für Verarbeitung und A für Ausgabe.

Mathematische Funktionsmaschine	E-V-A-Prinzip der Informatik

 

Prinzipiell werden in beiden Aufgabenstellungen Wert(e) aus einer festgelegten Menge (Definitionsmenge) aufgenommen und über eine Funktion zu einem eindeutigen Ergebnis verarbeitet, das am Ende ausgegeben wird. 

 

Videos zur Wiederholung des Funktionsbegriffs

Funktionsbegriff	Wertetabelle und Graph

 

 

Was ist also eine Funktion?

Eine Funktion ist eine Zuordnung, die

• jedem Element x aus der Definitionsmenge \(\small D_f\) der Funktion \( \small f\)
• eindeutig
• genau ein Element \(\small y=f(x)\) aus dem Wertebereich \(\small W_f\) der Funktion \( \small f\) zuordnet.
   
• \(\small y=f(x)\) wird auch der Funktionswert der Funktion \(\small f\) an der Stelle \( \small x\) genannt.

 

Funktion - Definitionsmenge - Wertemenge

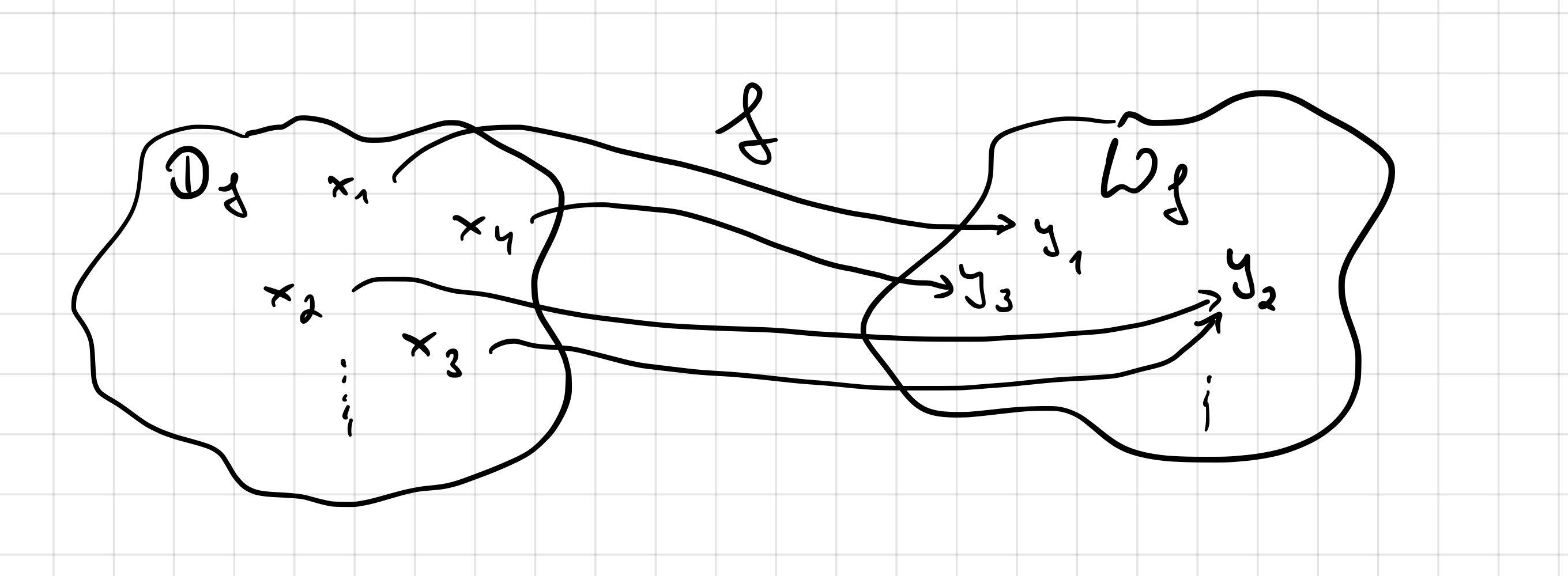
Erläuterungen:

• Für eine Funktion \(f\) gibt die Definitionsmenge \(D_f\) die Menge aller Zahlen an, für die jeweils ein Funktionswert berechnet werden soll bzw. darf.
•  Die Wertemenge \(W_f\) einer Funktion ist die Menge aller Funktionswerte, die aufgrund der Definitionsmenge berechnet werden konnte.

 

Wichtige Begriffe zu Funktion und Term

Als Basis legt die Zuordnungsvorschrift den Funktionsnamen, die Funktionsvariable (meist x) und den Bezeichner für die Funktionswerte (meist y) fest.

\(f:x \mapsto y\)

Die Funktionswerte y werden in der Regel mit einem Funktionsterm \(f(x)\) durch Einsetzen der jeweiligen x-Werte berechnet. Diesen Term gibt man teilweise auch anstatt y an.

\(f:x \mapsto f(x) \hspace{20mm}\)    z.B.:   \(f:x \mapsto x^2-6x+8\)

  

Die Funktion heißt in diesem Fall \(f\) und durch Einsetzen der x-Werte aus der Definitionsmenge \(D_f\) in den Funktionsterm werden die zugehörigen y-Werte berechnet.

  

Die Funktionsgleichung verdeutlicht einerseits dieses Berechnungsmuster und andererseits wird die Zusammengehörigkeit zweiter entsprechender Wertepaare \(x | y\) unterstrichen.

\(y=f(x)\hspace{20mm}\) oder \(\hspace{20mm} y=x^2-6x+8\)

 

Für eine Funktion \( \small f\) gibt die Definitionsmenge \(\small \mathbb D_f\) die Menge aller Zahlen an, für die jeweils ein Funktionswert berechnet werden soll bzw. darf.
Die Wertemenge \( \small \mathbb  W_f\) einer Funktion ist die Menge aller Funktionswerte, die aufgrund der Definitionsmenge berechnet werden konnten.

 

 

---