Ein
Kreisssektor ist eine
Teilfläche eines Vollkreises, die von einem
Kreisbogen \(b\)
und zwei daran anliegenden Strecken zum Kreismittelpunkt
\(M\) begrenzt wird.
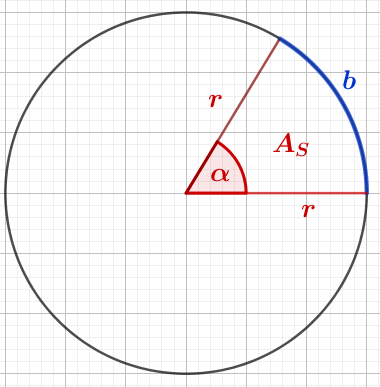
Die Fläche des Kreissektors \(A_S\) und die Länge des Kreisbogens \(b\) werden durch den Radius \(r\) und dem Mittelpunktswinkel \(\alpha\) bestimmt.
Beide Maße lassen sich aus der Fläche \(A_K\) und dem Umfang \(U_K\) des zuegörigen Vollkreises \(K\) ableiten!
Mit unserem Basiswissen für die Fläche eines Kreises \(A_K\) und dessen Umfang \(U_K\) können wir sehr schnell anschauliche Formeln für die Sektorfläche \(A_S\) und die Bogenlänge \(b\) herleiten, wenn wir beachten, dass der Mittelpunktswinkel eines Vollkreises \(\alpha=360°\) beträgt.
| Fläche eines Kreises | \(A_K = r^2 \cdot \pi \) |
| Umfang eines Kreises | \(U_K = 2 \cdot r \cdot \pi\) |
Für einen Kreissektor mit Mittelpunktswinkel \(\alpha = 1°\) erhalten wir jeweils \(\frac{1}{360}\) des Flächeninhalts bzw. des Umfangs eines Vollkreises.
\( \large \hspace{5mm} \Rightarrow A_S=\frac{1}{360} \cdot r^2 \pi \hspace{15mm} \) und \(\large \hspace{15mm} b=\frac{1}{360} \cdot 2r \pi \)
Für einen beliebigen Mittelpunktswinkel \(\alpha\) erhalten wir jeweils ein entsprechendes Vielfaches davon:
\(\large \hspace{5mm} \Rightarrow A_S=\alpha \cdot\frac{1}{360°} \cdot r^2 \pi \hspace{5mm} \) und \( \large \hspace{5mm} b=\alpha \cdot \frac{1}{360°} \cdot 2r \pi \)
|
Merke:
In einem Kreis mit
Radius \(r\) und Mittelpunktswinkel \(\alpha\) gilt für einen
Kreissektor:
|
Beispiel 1:
Für einen Kreissektor eines Kreises mit
Radius \(r=10 \space cm\) und dem Mittelpunktswinkel \(\alpha = 25°\) erhalten wir:
\(A_S=\frac{25°}{360°}\cdot (10 \space cm)^2 \cdot \pi=\frac{5}{72}\cdot 100 \space cm^2 \cdot \pi \approx 21,82 \space cm^2\)
\(b=\frac{25°}{360°}\cdot 2 \cdot 10 \space cm \cdot \pi =\frac{5}{72}\cdot 20 \space cm \cdot \pi\approx 4,36 \space cm\)
Beispiel 2:
Gegeben ist ein Kreissektor mit der
Fläche \(A_S=56 \space dm^2\) und dem Mittelpunktswinkel \(\alpha=40°\).
Berechne den Radius \(r\) des Kreises und die Bogenlänge \(b\) der Sektorfläche.
Ansatz mit der entsprechenden Flächenformel: \(A_S=\frac{\alpha}{360°}\cdot
r^2 \cdot \pi \)
Einsetzen der bekannten Werte und Auflösen der Gleichung nach \(r\):
\(56 \space dm^2=\frac{40°}{360°} \cdot r^2 \cdot \pi \hspace{10mm} | \space : (\frac{40°}{360°} \cdot \pi) \)
\( \frac{360° \cdot 56 \space dm^2}{40° \cdot \pi}=r^2 \hspace {5mm} \Rightarrow \hspace{5mm} r =\pm \sqrt{\frac{360° \cdot 56 \space dm^2}{40° \cdot \pi}}\approx \pm12,67 \space dm\)
Der Radius des Kreises beträgt also \(r \approx
12,67 \space dm\)
Für die Bogenlänge erhalten wir: \(b=\frac{40°}{360°} \cdot 2 \cdot 12,67 \space dm \cdot \pi \approx 8,85 \space dm \)
1.1 Kreisbogen