Funktionenschar einer verketteten Funktion

Nachfolgende Funktionenschar entsteht aus der Verkettung einer Polynomfunktion mit einer e-Funktion. In beiden Teilfunktionen finden wir den Scharparameter a.

Basis der Aufgabe: Abitur 2008 gk_Bayern!

•  \(f_a(x)=(2ax-2) \cdot e^{ax} \hspace{10mm}\) Funktionenschar mit Parameter a!
• \(g(x)=(4x-2) \cdot e^{2x} \hspace{16mm}\)  Repräsentant mit \(\space a=2 \)
• \(h(x)=(-4x-2) \cdot e^{-2x}\hspace{8mm}\)  Repräsentant mit \(\space a=-2 \)

Mit den Schieberegler lässt sich der Wert des Scharparameters \(a\) verändern und die Auswirkungen auf den Funktionsterm und Funktionsgraph werden direkt angezeigt.

Anstatt mehrere Funktionen für unterschiedliche Werte des Parameters a zu diskutieren, können wir die Funktionenschar analysieren und werden dabei feststellen:

• Jeder Graph der Schar hat im Punkt  \(\small P(0|-2)\)  vermutlich ein Minimum.
• Die Nullstelle hängt vom Scharparameter \(a\) ab,
• ebenso die Lage des Wendepunktes.
• Die Wendetangente lässt sich damit nur in Abhängigkeit des Parameters \(a\) bestimmen!

 

Diskussion der Scharfunktion

  
\(f_a(x)=(2ax-2) \cdot e^{ax} \hspace{3mm} mit \hspace{3mm}  D_f=R\)

 

---

Nullstellen:	\(f_a(x)=0 \Leftrightarrow\)	\( \space (2ax-2) \cdot e^{ax}=0\)
	\(e^{ax} > 0 \Rightarrow\)	\( \space (2ax-2) =0\)
	\(\Rightarrow\)	\(x_1=\frac{1}{a}\)
	Die Funktion hat den Schnittpunkt \(N_1(\frac{1}{a} | 0 ) \) mit der x-Achse, der vom Scharparameter a abhängt. Für \(|a| \rightarrow \pm \infty\)  wandert die Nullstelle zum Koordinatenursprung. Für \(|a| \rightarrow 0\) entfernt sich die Nullstelle vom Koordinatenursprung.

---

Extremstellen:	\( (u \cdot v)' = u' \cdot v + u \cdot v'\)	Ableiten mit der Produktregel! Kettenregel beim Ableiten des Terms \(e^{ax}\) nicht vergessen.
	\(f'_a(x)=0 \Leftrightarrow\)	\( \space 2a \cdot e^{ax}+(2ax-2) \cdot e^{ax} \cdot a=0\)
	\(e^{ax}\) ausklammern!  \(\Rightarrow\)	\(e^{ax}\cdot ( 2a +(2ax-2) \cdot  a=0\)
		\(e^{ax}\cdot ( 2a +2a^2x-2a)=0\)
	\(e^{ax} > 0 \Rightarrow\)	\( 2a^2x\cdot e^{ax} =0 \space \Leftrightarrow 2a^2x=0\)
	\(\Rightarrow\)	\(x_2=0\)  mit  \(y_2=f_a(0)=(2a \cdot 0-2) \cdot e^{a \cdot 0} =-2\)
	Unabhängig vom Parameter a haben alle Funktionen der Schar eine waagrechte Tangente an \(E(0 | -2 ) \). Die Art dieser Stelle, d.h. Minimum, Maximum oder Terrassenpunkt, ist noch mit einer Monotoniebetrachtung zu ermitteln.

---

       

Monotonie:	Mit Hilfe einer Monotoniebetrachtung wird das Steigungsverhalten der Funktion im gesamten Definitionsbereich analysiert: Die Nullstellen der ersten Ableitung zerlegen die Definitionsmenge in Teilintervalle. Nur an der jeweiligen Nullstelle kann eine Ableitung \(f'(x)\) ihr Vorzeichen ändern. Für jeden Teilintervall wird ein Zahlenwert von \(f'(x)\) berechnet und damit das Steigungsverhalten der Funktion bestimmt. Rückschlüsse auf die Art der  "Extremstelle" über das Steigungsverhalten!
	Monotoniebetrachtung:
	\(f_a(x)=(2ax-2) \cdot e^{ax}\)    mit  und	\(f'(x)=2a^2x \cdot e^{ax}\)   \(E(0 |-2)\)
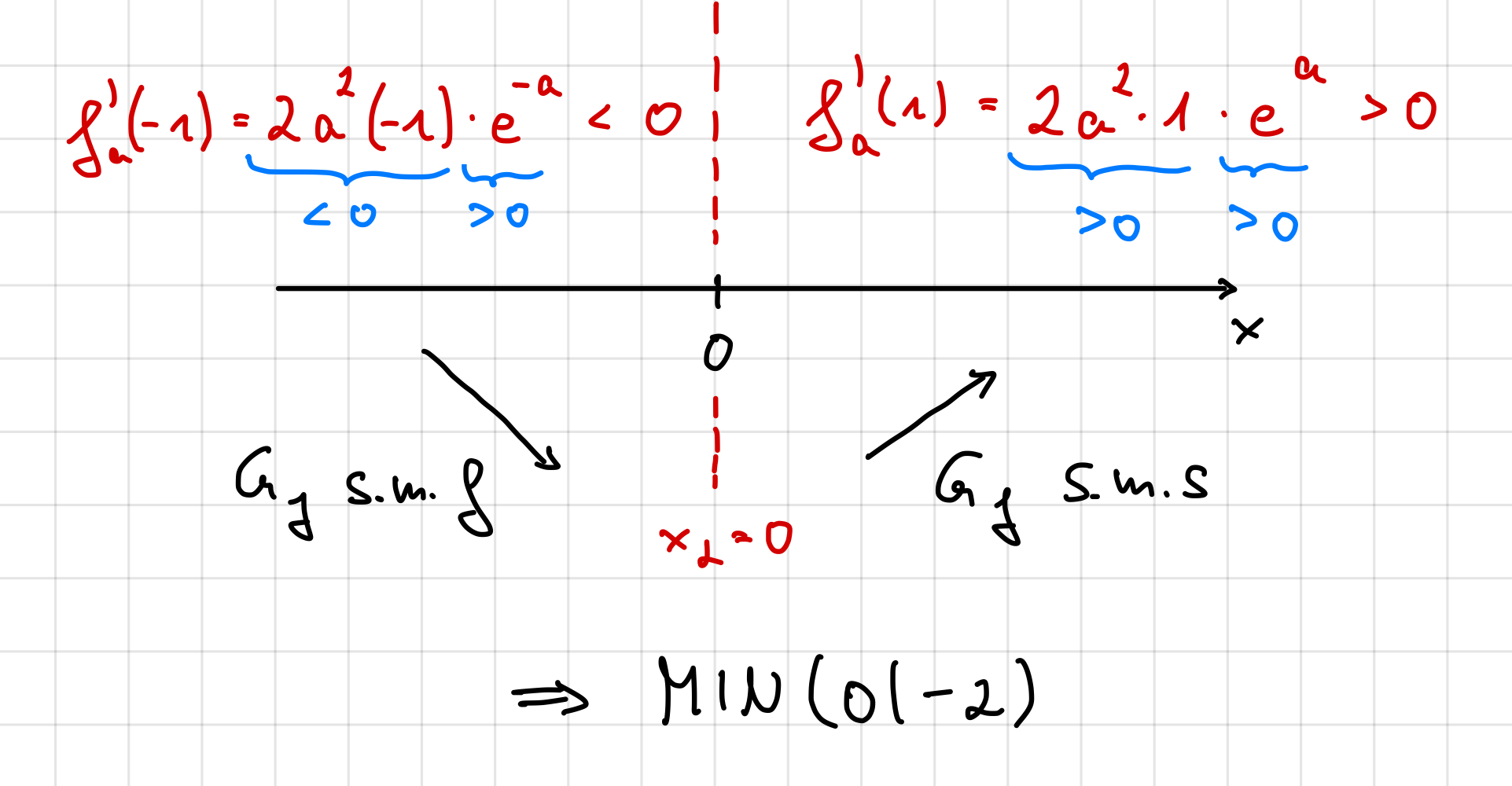
	Setzte aus dem jeweiligen Teilintervall einen beliebigen x-Wert in die Ableitungsfunktion ein. Das Vorzeichen bestimmt das Steigungsverhalten im gesamten Teilintervall. Ermittle daraus die Art der Extremstelle! In unserem Fall unabhängig vom Vorzeichen des Parameters a.

---