Bild_Oben

6.2 Bruchgleichungen und gebrochen rationale Funktionen

Die Schnittpunkte gebrochen rationaler Funktionen erhalten wir ebenso durch Gleichsetzen der Funktionsterme, was uns direkt zu den Bruchgleichungen führt.

Beispiel:

\( f(x)= \frac{2}{x}\)  
\( g(x)= \frac{4}{3-x} \)  

  

Gleichsetzen der Funktionsterme

\( \frac{2}{x}=  \frac{4}{3-x} \)

Alle Gleichungen, bei denen die Variable in mindestens einem Nenner auftritt, heißen Bruchgleichungen. Diese Gleichungen können rechnerisch und/oder graphisch gelöst werden und führen wieder zur Bestimmung des Schnittpunkts S der Funktionsgraphen.

 

Graphische Lösung

  • Zeichne die Funktionsgraphen der beiden Gleichungsseiten in ein Koordinatensystem.
  • Lies die Koordinaten des Schnittpunkts S (1 | 2) ab.
     
  • Die ursprüngliche Bruchgleichung

    \( \frac{2}{x}=  \frac{4}{3-x} \)

    hat also die Lösungsmenge  \(L=\{1 \} \)

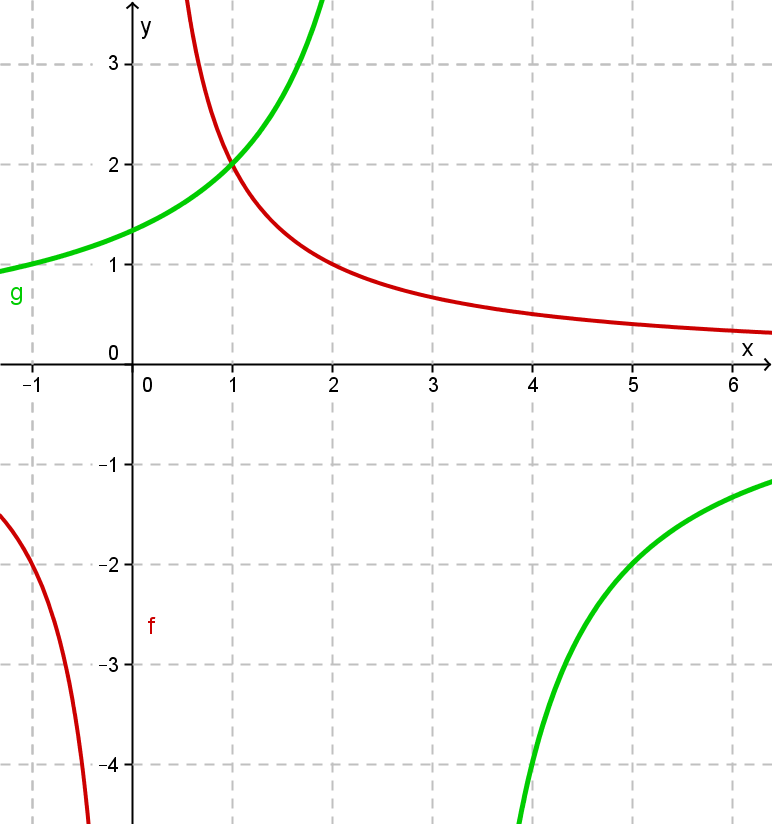 Schnittpunkt graphisch

 

Rechnerische Lösung
 Die rechnerische Lösung erfolgt in folgenden sechs Schritten:

  1. Bestimme die Definitionsmenge:  \(D=Q \setminus \{ 0 ; 3 \} \)
     
  2. Bestimme den Hauptnenner: HN \( = x \cdot (3-x) \)
     
  3. Multipliziere beide Seiten mit dem Hauptnenner:

    \( \frac{2}{x}=  \frac{4}{3-x} \hspace{1cm}  | \cdot x (3-x) \)

    \( \frac{2\cdot x \cdot (3-x)}{x}=  \frac{4\cdot x \cdot (3-x)}{(3-x)}   \)
     
  4.  Kürze so weit wie möglich:

    \( \frac{2 \cdot (3-x)}{1}=  \frac{4\cdot x }{1}   \)

    \( 2 \cdot (3-x) = 4x \)
     
  5. Löse wie üblich durch Äquivalenzumformungen

     \( 6-2x = 4x \hspace{1cm} \Rightarrow \hspace{1cm} x=1 \hspace{1cm} \Rightarrow \hspace{1cm} L=\{1 \} \)
     
  6. Setze das Ergebnis zur Probe in die Ausgangsgleichung ein:

 \( \frac{2}{1}=  \frac{4}{3-1} \)        Stimmt, die gesuchte Zahl ist 1.