6.1 Gleichungen und lineare Funktionen
Bei der Untersuchung linearer Funktionen haben wir festgestellt, dass
sich zwei Funktionsgraphen mit unterschiedlicher Steigung sicher in einem
gemeinsamen Punkt S,
dem sogenannten Schnittpunkt, schneiden.
Beispiel: Steigung der Graphen ist unterschiedlich
| \( f(x)= -\frac{2}{3}x+2
\) |
Steigung \(m_f = -\frac{2}{3} \) |
| \( g(x)= 2x-2
\) |
Steigung \(m_g = 2 \) |
Durch Gleichsetzen der Funktionsterme
erhalten wir den Ansatz zur rechnerischen und/oder
graphischen Bestimmung der Lösung.
\( -\frac{2}{3}x+2 = 2x-2 \)
|
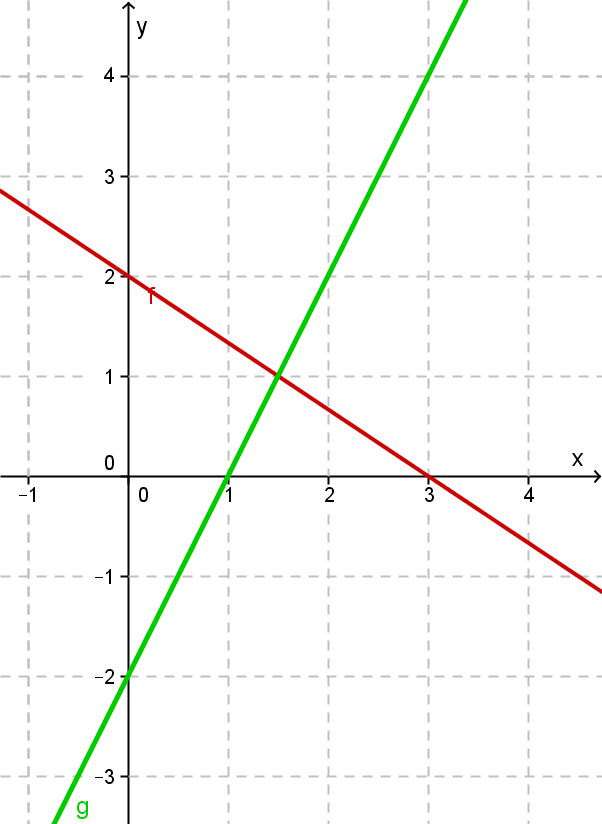
Graphische Lösung
- Zeichne die Funktionsgraphen der beiden Gleichungsseiten in ein Koordinatensystem.
- Lies die Koordinaten des Schnittpunkts S (1,5 | 1) ab.
- Die ursprüngliche Gleichung
\( -\frac{2}{3}x+2 = 2x-2 \)
hat also die Lösung \(L=\{1,5 \} \)
|
 |
|
Rechnerische Lösung
- Nach dem Gleichsetzen der beiden Funktionsterme kann die
entstandene Gleichung durch Äquivalenzumformungen nach x
aufgelöst werden.
\( -\frac{2}{3}x+2 =
2x-2 \)
| \( -2x - 2 \)
\( -\frac{8}{3}x = -4 \)
| \( : (-\frac{8}{3}) \)
\( x = 1,5 \hspace{1cm}
\Rightarrow \hspace{1cm} L=\{1,5 \} \)
- Durch Einsetzen des berechneten x-Wertes in eine der beiden
ursprünglichen Gleichungen wird der zugehörige y-Wert des
Schnittpunkts S berechnet.
\( x = 1,5 \) und
\( y = f(1,5 ) =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \)
S(1,5 | 1)
|


